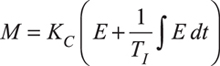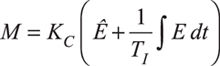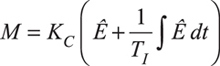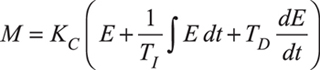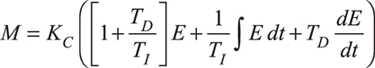Understand the common features and options that are often incorporated into digital implementations of the PID block.
Part 1 of this series of articles, which appeared in January, presented the basic equations for proportional-integral-derivative (PID) control (1). Part 2, in February, examined various aspects pertaining to the tuning parameters (2). This final installment of the series explains the features and options commonly provided by commercial process control systems. As is typical of digital technology, digital implementations of the PID control equations provide more features and options than their analog predecessors (3).
Reset feedback formulation
The relationships that comprise a PI controller can be expressed by an equation for the integral mode:

and an equation for the proportional mode:

where MR is the controller output bias, KC is the controller gain, TI is the integral time, E is the control error, and M is the controller output.
The input to the integral mode calculations is the control error, E. An alternative form, the reset feedback form, has the controller output, M, as the input to the integral mode calculations.
To obtain the reset feedback formulation, express the integral mode equation in the differential form:

From the proportional mode equation, replace KCE with (M – MR):

and rearrange Eq. 4 to:

Known as a first-order lag, Eq. 5 arises frequently in the context of process control. A common application is the exponential or lag filter used to smooth (attenuate) the noise that accompanies an input to the process controls.
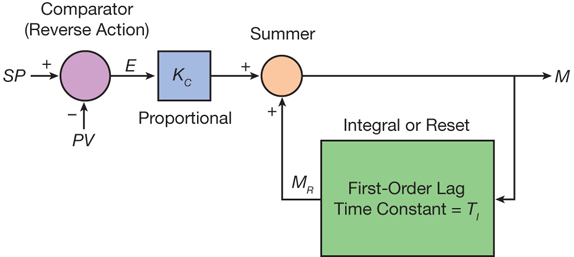
Figure 1. In this reset feedback implementation of a PI controller, the reset block obtains the controller output bias, MR, by filtering, or smoothing, the controller output, M, using the reset time, TI, as the time constant in the differential equation for the first-order lag.
Figure 1 depicts a reset feedback implementation of a PI controller. The summer implements the proportional mode equation. In the feedback path containing the reset block, the output of the summer, M, is the input to the reset block. The controller output bias, MR, is obtained by applying the first-order lag equation to the controller output, M. The reset time, TI, is the time constant for the first-order lag.
Part 1 of this series presented a computational procedure based on the difference equations for PID control. Briefly, for each iteration n, the procedure is: (1) start with values for the process variable, PV, on the current and previous iterations; (2) compute the rate of change of PV; (3) compute the projected value of PV; (4) compute the control error and projected control error; (5) apply integral action to obtain a new value for the controller output bias; and (6) apply the proportional-plus-bias equation to obtain the controller output on iteration n, Mn.
Step 5 of that procedure uses a difference equation for the reset mode to approximate integrating the control error:

To use the reset feedback form, only one change to that procedure is needed. To obtain the integral action, Eq. 6 is replaced by a difference equation for a first-order lag:
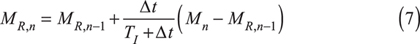
Most commercial digital process control systems integrate the control error, E (Eq. 6). A few, but not all, commercial control systems provide the option of using the reset feedback form.
In the analog world, performing the reset calculations by integrating E is impractical. All pneumatic and electronic controllers utilized the reset feedback structure in Figure 1, which is far easier to implement in analog circuitry.
Why is there interest in reset feedback? A feature known as external reset (briefly described later in this article) is unique to the reset feedback form of the PID control equation.
Parallel and series
Two slightly different approaches, one designated as parallel and the other as series, can be used to derive a PID control equation. Table 1 presents the equations for derivative based on E. The computations proceed as follows:
- Compute the control error, E.
- Compute the projected control error, Ê, using the following equation for derivative based on E (a similar approach can be used for derivative based on PV):

- PI control uses E in both the proportional and integral terms. To obtain PID control, the PI control equation can be computed with:
a. proportional based on Ê
b. integral based on E (parallel version) or on Ê (series version).
The only difference between the two PID equations is in the integral mode computations — the parallel version is based on the control error, E, and the series version is based on the projected control error, Ê. Equation 6 contains En, which indicates it is the parallel form. To obtain the series form, replace En with Ên.
The second and third rows of Table 1 show that algebraically substituting E + TD dE/dt for the projected control error gives the PID control equations in terms of E. The two equations are slightly different, but both are PID equations.
The parallel form of the PID control equation contains three distinct terms: proportional, integral, and derivative. At least conceptually, each term could be computed individually (or in parallel) and then added to obtain the controller output.
| Table 1. For PI control, the parallel and series equations are identical. For PID control, the only difference is that the parallel form integrates the control error, E, whereas the series form integrates the projected control error, Ê. When the equations are expressed in terms of E, the ratio TD/TI appears in the proportional term of the series equation. | ||
| Parallel | Series | |
| PI |
|
|
| PID in terms of E and Ê |
|
|
| PID in terms of only E |
|
|
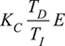
The computations for the series form can only be performed sequentially, i.e., in series. The series form of the PID control equation contains an additional component in the proportional term:
Adjusting the reset time...
Would you like to access the complete CEP Article?
No problem. You just have to complete the following steps.
You have completed 0 of 2 steps.
-
Log in
You must be logged in to view this content. Log in now.
-
AIChE Membership
You must be an AIChE member to view this article. Join now.
Copyright Permissions
Would you like to reuse content from CEP Magazine? It’s easy to request permission to reuse content. Simply click here to connect instantly to licensing services, where you can choose from a list of options regarding how you would like to reuse the desired content and complete the transaction.