Prevent Caking of Bulk Solids

Understanding the mechanisms behind caking, identifying key process variables and product specifications, and testing samples to predict the increase in cohesive strength of a powder over time are key to preventing and solving caking problems.

Caking occurs when powders, such as detergents, fertilizers, food powders, pharmaceutical formulations, and salts, that are stored at rest agglomerate. Caking problems can be challenging to solve, as agglomeration is not immediately evident. A product might have flowed easily during packaging, yet customers later report that the powder they received contains lumps. Operators who had no problems discharging powder from a silo when the plant was operating continuously might find that the same powder is difficult to discharge after the process had been shut down over a weekend.

The consequences of unintended agglomeration are not pleasant. Caking may cause customer dissatisfaction, followed by a decline in sales or a drop in productivity when product must be reworked. Caking can present a danger to plant personnel if caked material in a silo collapses.

The best metric for quantifying caking is not necessarily apparent. Those in charge of addressing a caking problem might attempt to count the lumps in a container of powder or record their size distribution. The investigator will quickly realize that the strength of the agglomerated material is important to measure, but how to quantify it is not always apparent. Any attempt to find the causes of caking is unlikely to succeed if a response to a change in a control variable cannot be measured.

Caking mechanisms

Caking results when the magnitude of interparticle forces increases over time. The adhesive forces are primarily van der Waals forces, polar interactions, and, when moisture is present, the forces associated with liquid bridges. Van der Waals forces include all intermolecular forces that act between electrically neutral molecules. Polar interactions occur when adjacent particles contain regions that are permanently electron-rich or electron-poor. Van der Waals forces and polar interactions are proportional to particle size and increase as the distance between particles decreases.

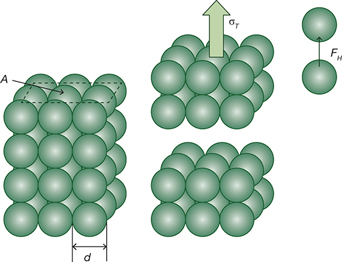
▲Figure 1. Tensile strength is proportional to the interparticle adhesive forces and the number of particle contacts, and inversely proportional to the particle diameter.

The likelihood of caking, however, generally decreases with increasing particle size. To understand the effect of particle size on agglomeration of powders, consider a compact of powder with a platen area A comprised of particles of diameter d, as illustrated in Figure 1(1). The tensile strength, σ_T, an indicator of a powder’s cohesiveness, is determined by measuring the force required to cause the compact to fail (deform) and dividing that value by the platen area.

Assuming that this force is equal to the sum of the adhesive forces, F_H, at the individual particle contacts, with n being the number of particle contacts:

The number of particle contacts is proportional to the platen area and inversely proportional to the square of the particle diameter:

So the tensile strength is inversely proportional to the particle diameter:

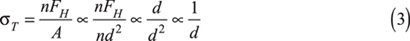
Thus, although interparticle forces increase with particle diameter, the strength of a powder, and thus its tendency to cake, decreases with increasing particle size.

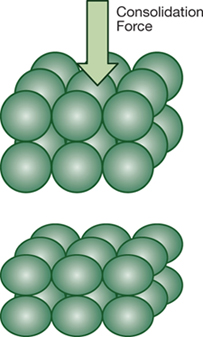
▶Figure 2. Plastic creep, or particle deformation, can occur at elevated temperatures or if impurities are present.

Some bulk materials can experience plastic creep if impurities (which may act as a plasticizer) are present or if the temperature increases. Plastic creep (Figure 2) is the deformation of a material under consolidation. Plastic creep can be severe in powders that are subjected to high temperatures for long periods of time, especially when they are above their glass transition temperature or at their melting point.

Liquid bridging occurs when moisture accumulates at the contact points between adjacent particles. The likelihood of liquid bridging can often be inferred from a powder’s moisture sorption isotherm, which relates relative humidity and equilibrium moisture content. Sorption isotherms are classified into five categories according to their shape and the process (2).

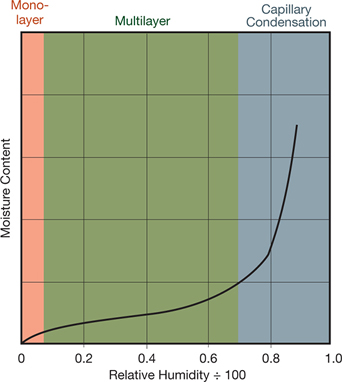
▲Figure 3. A powder’s moisture sorption isotherm can indicate the likelihood of liquid bridging. This isotherm (designated Type II because of its sigmoidal shape) characterizes a powder prone to caking.

Figure 3 is an example of a Type II isotherm, which has the sigmoidal shape characteristic of many powders prone to caking, such as lactose. At low relative humidity, the moisture isotherm is linear. In this region, water molecules are adsorbed until a monolayer forms. The effect of moisture on caking is generally negligible when moisture levels are very low. As relative humidity increases, hydrogen bonding produces multilayer adsorption. In this second region, the slope of the isotherm is initially shallow and then steepens with increasing relative humidity. As moisture uptake increases, the particles become surrounded by moisture. If the solids are water-soluble, the layer of moisture can be viscous, and the powder may become cohesive.

At high relative humidity, the equilibrium moisture content increases dramatically. In this region, most of the incremental condensation takes place at the contact points between particles. This phenomenon is known as capillary condensation. Capillary condensation is accompanied by liquid bridging, which creates strong forces between particles. Water itself is cohesive and adheres to the solid particle surfaces of many powders, especially those that are hygroscopic. Such powders can cake over time. If the liquid bridges contain soluble matter and the liquid evaporates, strong, solid bridges may form.

Strength also depends on the pressure (or stress) exerted on the powder during storage. The stress on solids in a cylinder increases with bed height. If a powder is packaged in a container with rigid walls, the stress profile is not linear, but instead depends on the height and cross-sectional area of the container and the friction between the powder and the container walls. The Janssen equation can be used to calculate the pressure profile in a container with vertical side walls (e.g., a cylinder or a box):

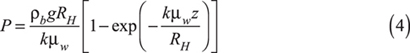
where P is the vertical solids pressure, ρ_b is the bulk density of the powder, g is the acceleration due to gravity, R_H is the hydraulic radius of the container, k is the Janssen coefficient (approximately 0.4 for many materials), μ_w is the wall friction coefficient, and z is the depth of the bulk material. Unlike a liquid’s pressure profile, which increases...