Capital cost estimation techniques in the chemical process industries (CPI) rely largely on scaling relationships. Understanding how scaling relationships relate to equipment characteristics enables you to use them more effectively, even when specific data is not available.
Put aside your graphing calculator and imagine for a minute that you are Ultraman — Japanese superhero, 40 m tall, battling oversized aliens to the delight of Tokyo’s schoolchildren. Your thighs measure a monstrous 6 m in diameter, but somehow your legs feel wobbly. Something is not right. You better get back to that calculator and run some numbers.
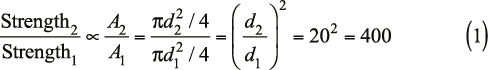
Ultraman is 20 times your height, but otherwise normally proportioned: His arms are 20 times the length of your arms, his bald spot is 20 times the diameter of yours, and so on. The strength (S) of a pillar is proportional to its cross-sectional area (A), which is equal to πd2/4, where d is the diameter. Based on this, you estimate that his legs are about 400 times as strong as yours:
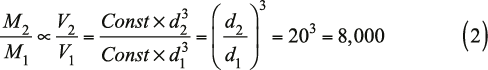
Ultraman’s mass (M) should be proportional to his volume (V). Just as area scales with the diameter squared, volume scales with the diameter cubed:
So, Ultraman is 8,000 times as heavy as you are, but only 400 times as strong. No wonder his legs seemed wobbly: Ultraman’s strength-to-weight ratio is only 400:8,000 = 5% of yours.
This inconvenient discovery is one implication of the mathematical principle Galileo called the square-cube law, which states that when an object grows, its volume grows faster than its surface area: if its length increases by a factor of x, its surface area will increase by a factor of x2 and its volume will increase by a factor of x3. This principle also explains why larger animals have a harder time cooling themselves than smaller ones, why you can drop an ant from almost any height without injuring it, and why larger cyclists tend to be faster in time trials than smaller ones.

This is expressed as:

or:

where l is a length. This equation is now in the form of a power scaling law. It is stated as “area scales with volume to the power of two-thirds,” and two-thirds is referred to as the scaling exponent. You could also say that “area is proportional to volume to the two-thirds:”
Since we live in three dimensions, most systems scale with exponents that are multiples of one-third...
Would you like to access the complete CEP Article?
No problem. You just have to complete the following steps.
You have completed 0 of 2 steps.
-
Log in
You must be logged in to view this content. Log in now.
-
AIChE Membership
You must be an AIChE member to view this article. Join now.
Copyright Permissions
Would you like to reuse content from CEP Magazine? It’s easy to request permission to reuse content. Simply click here to connect instantly to licensing services, where you can choose from a list of options regarding how you would like to reuse the desired content and complete the transaction.
