Adsorption Basics: Part 1

Adsorption can be used to treat waste streams or purify valuable components of a feed. This article describes both equilibrium and mass-transfer considerations, and reviews the fundamentals of adsorption system design.

Adsorption takes advantage of the tendency of one or more components of a liquid or gas to collect on the surface of a solid. This tendency can be leveraged to remove solutes from a liquid or gas or to separate components that have different affinities for the solid. The process objective may be either waste treatment or the purification of valuable components of a feed stream. In an adsorption process, the solid is called the adsorbent and the solute is known as the adsorbate.

Commercial adsorbents are highly porous, with pore surface areas ranging from about 100 to 1,200 m²/g. The large surface area allows a large amount of adsorption relative to the weight of the adsorbent, well in excess of its own weight in some cases. Moreover, solute levels in the treated fluid can be reduced to a fraction of a ppm.

The affinity of a fluid component for a particular adsorbent depends on molecular characteristics such as size, shape, and polarity, the partial pressure or concentration in the fluid, and the system temperature. The attraction is caused by van der Waals forces and hydrophobic inter-actions (not covalent bonding). Bonding energies in adsorption range from about 10 to 70 kJ/mol, much lower than typical covalent bond energies of 200 to 500 kJ/mol. The adsorption bonding energy is high enough for adsorption to occur, yet low enough to allow the adsorbent to be regenerated by removing the adsorbed molecules.

Equilibrium considerations

The adsorption process can be considered a partitioning of the adsorbate between the fluid phase and the adsorbent. If the solid and fluid are placed in contact for a long time, an equilibrium distribution is reached, and this equilibrium can be described quantitatively.

Equilibrium behavior is characterized by expressing the amount of adsorbate adsorbed as a function of partial pressure (gases) or concentration (liquids) at a fixed temperature. Such an equilibrium model is called an isotherm, and many have been proposed. The simplest, yet one that works surprisingly well for many systems (notably gases that are weakly adsorbed), is the Langmuir isotherm (1). This model assumes that the surface of the adsorbent is homogeneous and flat, that the adsorbate forms a single layer on the surface, and that there are no interactions between adsorbed molecules.

For a gas containing a single adsorbate, the Langmuir isotherm is:

where θ is the fraction of the total available adsorption sites that are occupied, K is the adsorption equilibrium constant, and p is the adsorbate partial pressure. Equation 1 is easily derived, as detailed in Ref. 2 and other sources.

At low partial pressures, the denominator approaches 1, and the fraction adsorbed varies linearly with partial pressure in what is known as the first-order region or the Henry’s law region. In this region, consistent with our intuition, a higher partial pressure increases the tendency toward adsorption.

However, as the pressure increases, the number of available adsorption sites decreases, and further adsorption becomes increasingly difficult. At high pressures, the denominator of Eq. 1 approaches Kp, and the fraction of occupied sites increases asymptotically to 1. Because there is little change in the amount of adsorbate adsorbed with pressure, this is called the zero-order region. Equation 1 also applies to liquids, with partial pressure replaced by concentration. The equations for multicomponent systems are given in Ref. 2.

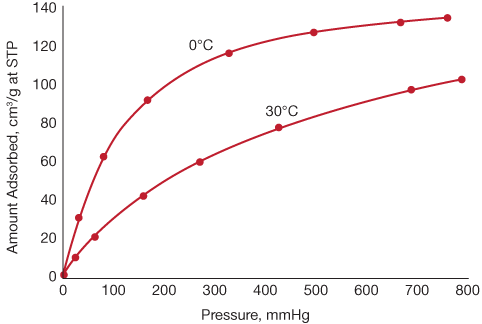
▲Figure 1. These data for the adsorption of ammonia onto charcoal follow the Langmuir isotherm reasonably closely. Data are from (3).

In practice, isotherms are usually expressed in terms of the amount of adsorbate adsorbed per unit weight of adsorbent, rather than the fraction of sites occupied. Such data are shown in Figure 1(3) for the adsorption of ammonia onto charcoal at two temperatures. These data follow the Langmuir model reasonably closely, and the first-order regions lie on the far left of the curves. The start of the zero-order region of the 0°C curve can also be seen, while the zero-order portion of the 30°C curve occurs at pressures higher than those shown.

Because the adsorption process is exothermic, the temperature significantly affects the amount of adsorbate adsorbed. In accordance with Le Chatelier’s principle, operation of exothermic processes at higher temperature favors conditions that evolve less heat. Consequently, at a given pressure, the amount of adsorbate adsorbed at equilibrium decreases with increasing temperature. For this reason, adsorption processes are usually operated at room temperature. The exception is viscous feeds such as sugar solutions, which are decolorized at elevated temperatures using activated carbon.

For situations where the Langmuir assumptions do not hold, numerous other models have been proposed. Most, like the Langmuir isotherm, contain first- and zero-order regions over certain ranges of partial pressure or concentration. One common model is the Freundlich isotherm:

where n is the weight adsorbed per unit weight of adsorbent, and k and m are temperature-dependent constants, with m usually between 1 and 5 (4). In general, k decreases and m increases with increasing temperature, which equates to less equilibrium adsorption. Note that this model does not contain a Henry’s law region at low pressures, except when m = 1 and the isotherm is linear. As with Eq. 1, pressure is replaced with concentration for liquids. The Freundlich isotherm works well for applications involving heterogeneous adsorbents — for example, adsorption of hydrocarbons by activated carbon.

Favorable and unfavorable isotherms are shown in Figure 2(5). A favorable isotherm is one that has a convex shape, representing a large amount of adsorption at a low partial pressure (or for liquids, concentration). Conversely, an unfavorable isotherm has a concave shape, and a relatively high partial pressure is needed to achieve economic adsorption. The ultimate in favorable isotherms is irreversible adsorption, where maximum adsorption is reached at very low partial pressures. Note that an isotherm that is favorable for adsorption is unfavorable for desorption. In particular, the most favorable isotherm is the most...