A Shortcut to Determine Optimal Steam Pipe Diameter

Existing models for calculating pipeline diameter are complicated and provide inconsistent and, therefore, unreliable outputs. This model simplifies the calculations to optimize the pipeline diameter and reduce overall plant cost.

Steam distribution pipelines are the necessary link between the steam boiler/generator and the steam user. An efficient steam distribution system is essential to deliver steam of the appropriate quality and pressure to the proper equipment. Installation and maintenance of the steam system are important issues that must be considered at the design stage. Both oversized and undersized pipelines can have operational problems. Pipes, valves, fittings, etc., in oversized pipelines will be more expensive than necessary, with higher capital and installation costs, and more support work and insulation. Additionally, in a system with oversized pipes, higher heat loss will produce a larger volume of condensate, which requires more steam trapping to avoid the delivery of wet steam.

The larger pressure drop of an undersized pipeline may limit the availability of lower-pressure steam to only the point of use, increasing the risk of erosion, water hammer, and noise due to the inherent increase in steam velocity.

Mathematically rigorous methods for selecting pipe diameters are time-consuming because they involve iterative procedures to determine the minimum total capital and operating costs. Simple equations can provide reasonably accurate estimates of optimum pipe diameters in the initial stages of a design, which can serve as a good starting point for a more rigorous procedure.

The first pipeline optimization model based on economics initially applied to turbulent flowing fluids in hydraulically smooth pipes, and it was later broadened to accommodate laminar flow; a new model was recently developed for hydraulically rough pipes. All of these models were developed for fluids that receive energy from pumps, compressors, blowers, or fans that are powered by electric motors, so none of them can be used for steam pipelines (1–3).

This article presents a simple optimization model to estimate the diameter of steam pipelines, and discusses the role of parameters such as plant location and fuel type. Two example calculations compare the recommended steam velocities in the literature and the solutions obtained from the proposed model.

A model based on economic criteria

Economic criteria are crucial for plant design in various engineering fields. Optimizing the size of plant equipment ensures the lowest lifecycle cost of any project. The cost of piping can represent up to 35% of plant capital cost. Therefore, it is useful to optimize piping systems to reduce capital and pumping costs.

Determining pipe cost requires considering both the capital and operational costs. Although the capital cost is the primary consideration for most projects, engineers should be aware that the most economic pipe diameter will be the one with the lowest total cost throughout the lifetime of the project, which incorporates annual maintenance costs. Although there are steam pipelines more than a century old that are still operating, most are predicted to last about 20 years.

Capital cost of a pipeline

For pipe with an internal diameter D (m) and length L (m), purchase cost, C_P, can be expressed by (1):

where m and n are parameters based on the type of pipe material and pipe wall thickness (pipe schedule), respectively; market prices determine the values of m and n for each country. Pipe cost is theoretically proportional to pipe diameter per square area. This is not true for real pipe prices.

The annual maintenance cost of a pipeline, b, is commonly expressed as a fraction of capital costs, so with an amortization rate of a, the annualized capital cost, C_c, of a pipeline can be calculated by:

where F is the factor that includes the cost of valves, fittings, and construction.

Pipeline operating cost

The operating cost of a pipeline depends on the energy consumption necessary to achieve fluid flow through the pipeline.

The energy balance of any flow system includes specific energies calculated at the system inlet and outlet. A general form of the energy balance equation is:

Energy_in + Generation = Energy_out + Consumption + Accumulation

For steady-state processes, the accumulation of energy is zero, and for insulated pipelines, heat loss through pipe walls is negligible, so the energy balance equation for a pipeline is simplified to:

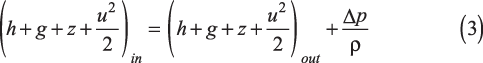
where h (J/kg) is specific enthalpy, g (m/sec²) is gravitational acceleration, z (m) is height above an arbitrary datum, u (m/sec) is velocity, Δp (Pa) is pressure drop, ρ (kg/m³) is fluid density, and in and out are indices denoting inlet and outlet conditions of the pipeline. The term Δp/ρ denotes the energy lost due to fluid friction.

In steam pipelines, the steam is usually superheated or saturated. If the change in fluid expansion due to a pressure drop is neglected, the horizontal pipeline transport from Eq. 3 becomes:

The boiler duty, Q (W), is:

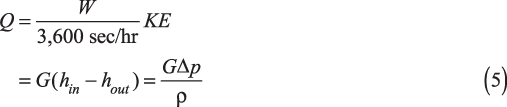
where G (kg/s) is the mass flowrate of steam, W (kg/hr) is fuel consumption, K (J/kg) is the lower heating value of fuel, and E is boiler efficiency.

Pressure drop is calculated as the sum of frictional pressure drop, Δp_fr (Pa), and minor pressure losses, Δp_ml (Pa):

The Weisbach equation for friction pressure drop is:

where ξ is the Darcy friction factor.

Minor pressure losses can be estimated either as head losses or by using equivalent lengths. In further analysis, minor pressure losses will simply be taken into account by:

where J is the ratio of minor pressure losses to frictional pressure drop.

Equations 7 and 8 apply to incompressible isothermal fluid (liquid) flow. In engineering practice, this equation is acceptable for compressible fluid (gas) flow if the total pressure drop is less than 10% of the initial pressure.

If the plant operates Y hr/yr, the annual operational cost (C_e) of the steam line is:

which can be written as:

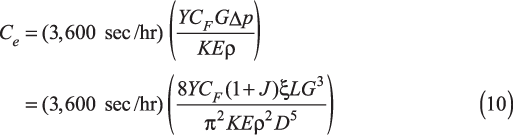
where C_F ($/kg of fuel) is the cost of fuel.

Optimizing...