CFD-DEM: Modeling the Small to Understand the Large

Coupling the traditional computational fluid dynamics (CFD) approach to model the fluid phase with the discrete element method (DEM) to model the particles creates a powerful numerical method to study multiphase particulate flows.

Computational fluid dynamics (CFD) emerged in recent decades and reduced the costs associated with scale-up, optimization, safety analysis, and industrial operations that involve conventional fluids. It provides numerical information that enhances and supplements experimental data and eliminates the need to rely entirely on expensive experiments to gather data that are hard or impossible to measure directly. For example, CFD simulations allow engineers to isolate the effects of a single variable, whereas in experiments, it may be impractical to change only one variable at a time.

For the numerical simulation of solids flows, a counterpart to CFD is the discrete element method (DEM), which tracks the motion of every particle by solving Newton’s equations of motion for particles in free flight and employs a collision model for the particles in contact (1). Numerous collision models exist and incorporate the conservation of momentum and kinetic energy loss due to inelasticity and/or friction. It is relatively straightforward to incorporate microscale physics such as cohesion into the DEM framework because each contact is resolved (2).

Multiphase flows — which are pervasive throughout the chemical, petrochemical, energy, pharmaceutical, mining, and other key industrial areas — present an additional challenge to numerical analysis. Specifically, gas-solid particulate flows pose challenges related to interfacial interactions (heat and mass transfer, chemical reactions, etc.), instabilities (clustering and bubbling), multiscale phenomena (particle-scale physics affecting system-scale operation), and locally defluidized regions (enduring and multiparticle contacts), among others.

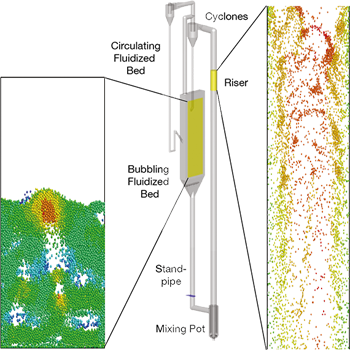
▲Figure 1. DEM simulations are capable of modeling subsystems or high-consequence regions. Displayed here are snapshots from DEM simulations of dense gas-solid flow in the bubbling bed of a circulating fluidized bed (CFB) and dilute gas-solid flow in the riser of a CFB.

Researchers have coupled CFD for the gas phase with DEM for the particulate phase to tackle the challenges of gas-solid flows. The use of this CFD-DEM method has ballooned in recent years, especially within the academic community (as evidenced by the rapid increase in publications on the topic). CFD-DEM strikes a better balance between numerical accuracy and computational requirement than direct numerical simulation (DNS) and coarse-grained methods (discussed later). However, the biggest barrier to widespread adoption by industry is the computational overhead of CFD-DEM, which remains an issue for larger multiphase systems. While modeling every particle in a very large industrial unit will remain impractical for the foreseeable future, simulating subsystems and other high-consequence regions is currently possible (Figure 1). Additionally, as the parallel capability of computers continues to advance, the number of particles CFD-DEM is capable of handling also continues to rise, making it a promising tool to aid in the design of many industrially relevant problems.

This article provides a general overview of several key methods used for the numerical simulation of gas-solid multiphase flows and explains where CFD-DEM fits into the picture. It discusses the current state of the art of CFD-DEM, with an emphasis on the main challenges and bottlenecks, and outlines areas for improvement aimed to address industrial needs.

Computational methods for gas-solid flow

The prediction of multiphase fluid-particle flows is an inherently multiscale problem. Industrial applications involve behavior on the order of meters to tens of meters. Unfortunately for industrial practitioners, bubbling and clustering instabilities at the mesoscale (appreciably larger than the particle scale, yet still significantly smaller than the system scale) strongly influence macroscale behavior. In addition, interfacial phenomena — mass, momentum, and heat transfer — that occur at the microscale (i.e., tens to hundreds of particles) influence mesoscale behavior. Furthermore, truly microscopic properties, such as particle surface roughness and humidity in a gas carrier phase, can also influence behavior at the mesoscale and beyond. Reference 3 provides an interesting case study that illustrates how microscopic properties affect macroscopic behavior.

▲Figure 2. Different numerical methods are available to simulate particle systems depending on system size. (a) Direct numerical simulation (DNS) is appropriate for studying the detailed (microscale) gas flow field around particles. Image of flow around a fixed bed of particles courtesy of S. Subramaniam, et al. At the mesoscale, the local gas flow is resolved down to a scale of several particle diameters (flow around an individual particle is not resolved): CFD-DEM simulates a gas-solid homogeneous cooling system in a clustered state (b) and a fully resolved two-fluid model (TFM) simulates unbounded fluidization (c). Macroscale methods include filtered TFM, energy minimization multiscale simulation (EMMS), and multiphase particle in cell (MP-PIC), which is used here to model a fluidized catalytic cracking (FCC) catalyst in a pilot-scale (3-ft-dia.) fluidized bed with an air sparger (d). Contours show gas-velocity magnitude in (a) and (b) and solids concentration in (c) and (d); hot colors (red) indicate high values and cool colors (blue) indicate low values, and in (a) and (b), white indicates the interior of (monodispersed) particles.

As a consequence of this multiscale nature, no single numerical method can directly simulate the wide range of scales needed to completely model the dynamics of particulate flows. Instead, researchers have developed a multitude of different methods to handle different scales. The higher-resolution methods are more reliable and desirable, because fewer constitutive relations, which are inherent sources of uncertainty, are needed to close the model. The trade-off is that higher resolution comes at an increased computational cost. Figure 2 compares some of the numerical methods commonly used to study fluid-particle flow.

Continuum methods

Since industrial processes often involve many particles, continuum approaches that only attempt to solve for the bulk behavior are the preferred approach for modeling large-scale systems. A two-fluid model (TFM) or Eulerian-Eulerian (E-E) model simulates both the actual (molecular) fluid phase and the solids phase (a “fluid” composed of the particles) with independent Navier-Stokes-like equations (e.g., continuity, momentum, energy) weighted by the fluids’ volumetric concentration and connected through interfacial transfer phenomena (e.g., phase change, drag, etc.). In addition to the interfacial transfer terms, TFMs require the user to specify unknown quantities such as solids-phase pressure and viscosity — opening the door for significant uncertainties.

A kinetic theory (KT) approach (4) is commonly used to derive such constitutive expressions, particularly when the fluid phase is a gas (5). Recent efforts have shown that the results obtained with KT-based TFMs compare favorably to more-accurate discrete particle data (6, 7). However, a grid resolution of approximately ten times the particle diameter (Δ_x ~ 10d_p) is still required to resolve all scales of motion relevant to cluster dynamics (8). Even finer resolutions are required in dense beds that exhibit bubbling (7), because sharp gradients can exist at the cluster/dilute or the emulsion/bubble interfaces.

Since instabilities in gas-particle flows are ubiquitous in industrial devices (9), high-resolution TFM simulations (sometimes referred to as KT-TFM or microscopic TFM) are too computationally intensive for most industrial applications. An additional level of averaging is required to tackle industrial-scale problems. One common strategy is filtered-TFMs (10–12). Filtered-TFMs rely on an averaging procedure similar to the filtering of the Navier-Stokes equations for single-phase large-eddy simulation (LES). However, in multiphase flows, many more sub-grid-scale closures are needed. Although filtered-TFM methods have been applied successfully to many cases, robust model development remains an active area of research.

Discrete methods

Unlike the continuum approach for solids described previously, discrete methods treat the particles as discrete entities. The coupled approach that combines a discrete method for particles and a continuum model for the fluid is referred to as a Eulerian-Lagrangian (E-L) method. Two treatments of the fluid phase are common, DNS and CFD-DEM.

In DNS, all scales of fluid motion are resolved down to the no-slip boundary condition on the surface of each particle. No closure laws are required; drag is an output rather than a required input. Consequently, the Eulerian grid needs to be smaller than the particles, and resolutions on the order of Δ_x ~ d_p/10 are typically required to resolve such fine details for flows with moderate particle-Reynolds numbers. An approach with such fine resolution is extremely computationally expensive. Thus, DNS is unlikely to make a significant industrial impact for some time. For moving particle suspensions (as opposed to fixed-bed simulations, where the particles are static), current DNS capabilities allow for simulations of a few thousand particles. Reference 13 provides a comprehensive review of particle-laden DNS.

A less computationally expensive approach is to use a larger grid for the fluid phase while still using DEM to track the...