(388g) Bayesian Optimisation for Plug Performance of Coiled Tubes at Low-Reynolds-Number

Coiled tubes are used in polymerisation [1], nanoparticles synthesis [2], biotherapeutics [3], and heat-exchanger systems [4], due to their desirable plug flow capability. Plug flow is characterised by strong radial mixing and reduced axial mixing due to the formation of Dean vortices [5]. Typically, plug flow characteristics are only observed in coiled tubes when Re>300 unless an oscillatory motion is superimposed. This enables plug flow under highly-laminar Reynolds numbers (at least as low as Re=10) [6],[7]. The combination of Reynolds number, oscillation conditions (frequency/amplitude) and tube geometry (tube diameter, radius of curvature and pitch) leads to a high-dimensional parameter space that likely contains an optimal configuration to maximise the plug flow performance and mixing response.

Experimental and Computational Fluid Dynamics (CFD) studies have revealed that the mixing efficiency is sensitive to the coil geometry. Increasing the tube diameter and coil’s pitch, or decreasing the radius of curvature all improve the mixing efficiency since these parameters affect Dean vortex formation [8], [9]. Additionally, it has been observed that increasing the oscillation amplitude and frequency causes the plug flow to ‘switch on’ then ‘switch off’, indicating an optimal operation region must exist. Understanding how the geometric and operating condition parameters interact to produce the plug flow response is critical. However, exploration of the vast parameter space via experiments is expensive. Instead, CFD is an attractive low-cost alternative for parametric analysis, though the choice of an optimisation algorithm can offset the benefits.

CFD based optimisers are largely gradient-based using an adjoint method [10], which although quick in finding local optima, does not guarantee the detection of global optimality. Another option is genetic algorithms for multi-objective optimisation within the gradient-free black-box optimisation technique. Whilst the end results are promising, this method requires very large numbers of CFD runs (order of 1,000’s) to be performed and evaluated, which removes the cost and time advantage [11]. Another possibility is to replace expensive CFD simulations with cheap surrogate models, such as neural networks, regressions or radial basis functions [12]. However, this method can only start the optimisation process after building the surrogate model using the generated results from CFD, which still increases the number of CFD simulations. Therefore, in this study, we explore Bayesian optimisation to optimise the oscillatory helical coils because it has been proven to find optimal solutions with minimal parameter data [13] [14].

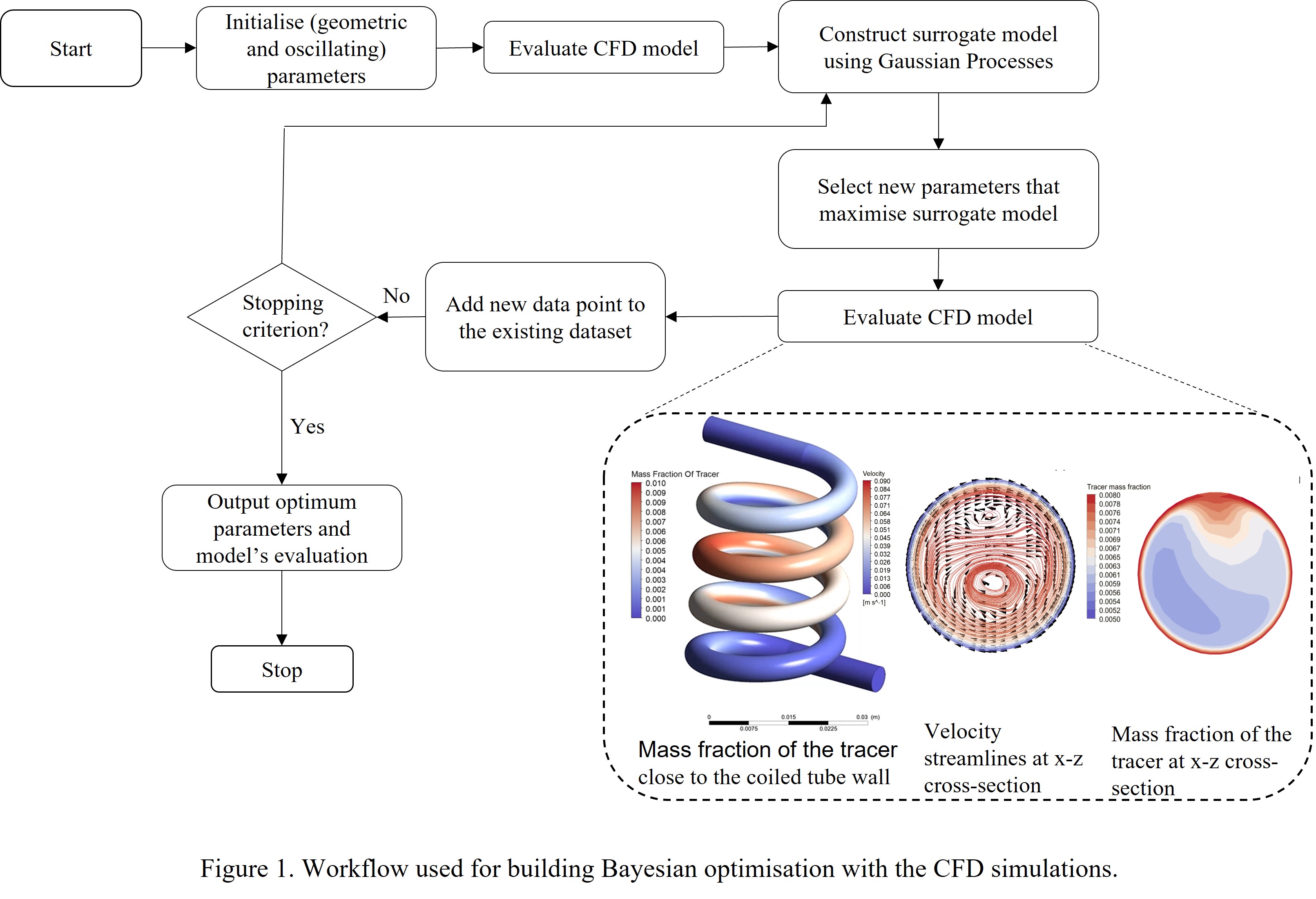
We deploy a black-box Bayesian optimisation technique coupled with a computational fluid dynamics (CFD) model in coiled tubes subject to oscillatory flows. The Bayesian exploration uses the Gaussian process as a surrogate model, and we integrate this with the OpenFOAM solver through the PyFoam library. The parametric geometries are generated using FreeCAD through Python script. We run transient CFD simulations of tracer injections into the water medium with scalarTransportFoam to track the tracer concentration in the tube. The groovyBC boundary-condition is introduced for imposing oscillatory velocity at the inlet. The plug flow performance is evaluated through residence time distribution (RTD), and the curve from the tank-in-series model is matched against this RTD to find the number of equivalent tank-in-series (‘N’). The workflow for the model is shown in Figure 1. The CFD model is used to evaluate N as a function of the geometric and oscillating input parameters as well as underlying vortex structures corresponding to the input parameters and N value. Better plug flow performance (equivalent to a higher value of N, with N = 10 considered the minimum standard) corresponded to Dean vortices filling the entire radial cross-sectional area of the tube leading to effective radial mixing. We validated the computational RTDs against experimental data. The results show a significant improvement in plug flow performance for only a slight variation in parameters, particularly the oscillation frequency and amplitude at a fixed geometry.

We achieved an open-source, automated, closed-loop model capable of finding optimal solutions through this study. This shows the potential of applying a data-driven model to efficiently explore high-dimensional parameter spaces that are otherwise too expensive using CFD or experiments alone. We anticipate that this modelling approach can lead to better process efficiency and perhaps bespoke coiled tube designs tailored towards targeted processes.

References

[1] D. Parida et al., “Coil flow inversion as a route to control polymerization in microreactors,” Macromolecules, 2014, doi: 10.1021/ma5001628.

[2] K. J. Wu, G. M. De Varine Bohan, and L. Torrente-Murciano, “Synthesis of narrow sized silver nanoparticles in the absence of capping ligands in helical microreactors,” React. Chem. Eng., 2017, doi: 10.1039/c6re00202a.

[3] N. Kateja and A. Rathore, “Spiralling into affordable healthcare,” The Chemical Engineer, pp. 33–35, 2018.

[4] J. Singh and K. D. P. Nigam, “Pilot plant study for effective heat transfer area of coiled flow inverter,” Chem. Eng. Process. Process Intensif., 2016, doi: 10.1016/j.cep.2016.02.001.

[5] A. K. Saxena and K. D. P. Nigam, “Coiled configuration for flow inversion and its effect on residence time distribution,” AIChE J., 1984, doi: 10.1002/aic.690300303.

[6] J. A. Koutsky and R. J. Adler, “Minimisation of axial dispersion by use of secondary flow in helical tubes,” Can. J. Chem. Eng., 1964, doi: 10.1002/cjce.5450420602.

[7] J. R. McDonough, S. Murta, R. Law, and A. P. Harvey, “Oscillatory fluid motion unlocks plug flow operation in helical tube reactors at lower Reynolds numbers (Re ≤ 10),” Chem. Eng. J., vol. 358, no. July 2018, pp. 643–657, 2019, doi: 10.1016/j.cej.2018.10.054.

[8] M. Mansour, P. Khot, D. Thévenin, K. D. P. Nigam, and K. Zähringer, “Optimal Reynolds number for liquid-liquid mixing in helical pipes,” Chem. Eng. Sci., 2020, doi: 10.1016/j.ces.2018.09.046.

[9] M. Mansour et al., “Numerical study of liquid-liquid mixing in helical pipes,” Chem. Eng. Sci., 2017, doi: 10.1016/j.ces.2017.06.015.

[10] J. G. Williams, F. Wechsung, B. W. Turney, S. L. Waters, and D. E. Moulton, “Shape optimisation for faster washout in recirculating flows,” J. Fluid Mech., 2021, doi: 10.1017/jfm.2020.1119.

[11] M. Mansour, K. Zähringer, K. D. P. Nigam, D. Thévenin, and G. Janiga, “Multi-objective optimization of liquid-liquid mixing in helical pipes using Genetic Algorithms coupled with Computational Fluid Dynamics,” Chem. Eng. J., 2020, doi: 10.1016/j.cej.2019.123570.

[12] D. Misiulia, K. Elsayed, and A. G. Andersson, “Geometry optimization of a deswirler for cyclone separator in terms of pressure drop using CFD and artificial neural network,” Sep. Purif. Technol., 2017, doi: 10.1016/j.seppur.2017.05.025.

[13] D. van de Berg, T. Savage, P. Petsagkourakis, D. Zhang, N. Shah, and E. A. del Rio-Chanona, “Data-driven optimization for process systems engineering applications,” Chem. Eng. Sci., 2022, doi: 10.1016/j.ces.2021.117135.

[14] S. J. Daniels, A. A. M. Rahat, R. M. Everson, G. R. Tabor, and J. E. Fieldsend, “A suite of computationally expensive shape optimisation problems using computational fluid dynamics,” 2018, doi: 10.1007/978-3-319-99259-4_24.