(234b) An Implicit Function Formulation for Optimization of Discretized Index-1 Differential Algebraic Systems

Differential algebraic equations (DAEs) are an expressive class of equations for
chemical and process systems engineers. They are capable of representing
processes that evolve over continuous time and/or space domains and involve
nonlinear physical and chemical phenomena.
Complicated interactions among differential states are often described
by large numbers of highly nonlinear algebraic equations that represent the
thermodynamics, chemical reactions, and transport phenomena of the system.
Due to their number and complexity, the ability to simulate or optimize
a large-scale DAE relies heavily on the ability to converge these
algebraic equations.
This work focuses on the optimization of DAE systems via second-order
local optimization methods.

Two contrasting approaches for DAE optimization are sequential, in which
the DAE is simulated each iteration of the optimization algorithm,
and simultaneous, in which the discretized DAE is converged during
the optimization algorithm.
Typically, sequential approaches are more robust while simultaneous approaches
are less time-consuming.
Simultaneous approaches are popular and accessible due to the availability
of modeling and discretization tools
such as IDAES [1], Pyomo.DAE [2], and InfiniteOpt
[3], which are built on top of the algebraic modeling
environments Pyomo and JuMP.
Hybrid approaches, including multiple-shooting, have also been proposed and may
offer a balance of convergence reliability and solve time.

We propose a simultaneous (fully-discretized) approach in which algebraic
equations are converged in an implicit function. This approach relies on the
index-1 property of the DAE system and uses the implicit function theorem
to automatically calculate exact first and second derivatives, which are sent
to a nonlinear optimization algorithm.
We expect this formulation to yield more reliable convergence as
removing the algebraic variables and equations from the optimization
formulation leaves it less likely to encounter regions of severe
ill-conditioning or degeneracy that can lead to non-convergence.
We implement this formulation using PyNumero [4],
a Pyomo extension for high-level implementation of nonlinear optimization
algorithms with efficient scale-dependent numerical computations.
To demonstrate the potential of this formulation to yield more reliable
solver convergence, we solve instances
of a chemical looping combustion (CLC) dynamic optimization problem from
IDAES with IPOPT.
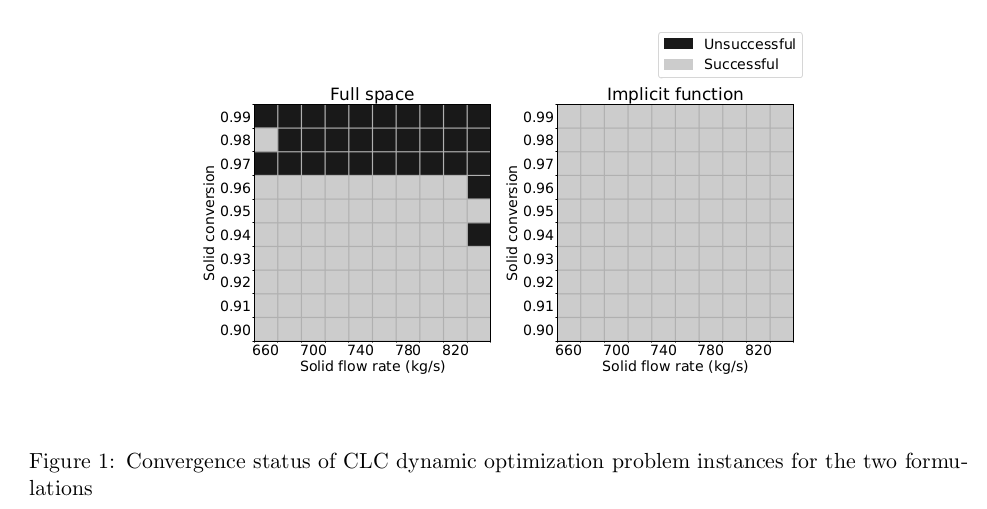
Our results, which are shown in Figure 1 for a parameter
sweep of instances parameterized by solid inlet flow rate and solid
conversion, demonstrate significantly improved convergence reliability
over the full-space simultaneous formulation
without an associated increase in solve time.
In this set of 100 instances, the implicit function formulation converges
all 100 instances in an average of 64 s, while the full space formulation
converges 69 out of 100 instances in an average of 83 s.

In this talk, we describe our formulation, including methods for function
and derivative calculations, give the details of our implementation
in the PyNumero software framework, and describe our results on a
distillation column dynamic optimization problem, a CLC steady state
simulation problem, and a CLC dynamic optimization problem.

[1] Andrew Lee, Jaffer H. Ghouse, John C. Eslick, Carl D. Laird, John D. Siirola, Miguel A.
Zamarripa, Dan Gunter, John H. Shinn, Alexander W. Dowling, Debangsu Bhattacharyya,
Lorenz T. Biegler, Anthony P. Burgard, and David C. Miller. The IDAES process modeling
framework and model libraryFlexibility for process simulation and optimization. Journal of
Advanced Manufacturing and Processing, 3(3):e10095, 2021.
[2] Bethany Nicholson, John D. Siirola, Jean-Paul Watson, Victor M. Zavala, and Lorenz T. Biegler.
pyomo.dae: A modeling and automatic discretization framework for optimization with differ-
ential and algebraic equations. Mathematical Programming Computation, 10(2):187–223, 2018.
[3] Joshua L. Pulsipher, Weiqi Zhang, Tyler J. Hongisto, and Victor M. Zavala. A unifying modeling
abstraction for infinite-dimensional optimization. Computers & Chemical Engineering, 156,
2022.
[4] Jose Rodriguez, Robert Parker, Carl Laird, Bethany Nicholson, John Siirola, and Michael
Bynum. Scalable Parallel Nonlinear Optimization with PyNumero and Parapint, 2021. Preprint
at http://www.optimization-online.org/DB HTML/2021/09/8596.html.