(12h) Latent State Space Modeling of High-Dimensional Data in Chemical Systems

Data from chemical processes are usually in high-dimensional time series forms. With the fast development of process industries, the high-dimensional, collinear, and dynamic characteristics in industrial time series are more pronounced for autonomous systems (Esptein and Pojman, 1998), where sensor redundancy is necessary to be foolproof and tolerant to failures. The redundancy can make the dimension of the observed features much larger than that of the dynamics, which poses challenges to traditional time series and system identification methods that assume full-dimensional dynamic excitation in the process data. It is therefore critical to develop new methods to develop reduced-dimensional dynamic models for monitoring, control, and decision making in chemical plants (Qin et al., 2020).

Principal component analysis (PCA), partial least squares (PLS), and canonical correlation analysis (CCA) are classical reduced-dimensional latent space models that have been widely used for data analytics in chemical processes (Jolliffe and Cadima, 2002, Krämer and Sugiyama, 2011, Negiz and Çlinar, 1997). These linear models project data from the original space into a reduced-dimensional latent space such that the projected latent variables capture the maximum variance, covariance, or correlations, but they do not focus on the predictability of the extracted latent variables.

In multivariate time series analysis, some linear combinations of the variables were first recognized could be serially uncorrelated, even though each individual variable is serially correlated (Box and Tiao, 1977). They further applied canonical analysis to decompose the time series residuals into dynamic and static latent factors. Pena and Box (Pena and Box, 1987) illustrated that the serially uncorrelated factors and dynamic factors co-exist in latent system structure with multivariate time series data.

Dynamic factor models (DFM) have been studied extensively in high-dimensional time series to extract reduced-dimensional dynamic factors based on time-lagged auto-covariance matrices of the multivariate time series (Lam and Yao, 2012). An improved time-domain approach enforces causal relations (Peña et al., 2019), where only past and current data are used in the model. One limitation of these methods is that they correspond to covariance-based objective functions that yield consistent estimates, but not necessarily efficient ones. Further, these methods do not automatically lead to an explicit dynamic latent variable (DLV) model; a follow-up step has to be employed to build vector auto-regressive DLV models.

The above DFM methods are related to subspace identification methods (SIM). However, SIMs extract state variables rather than latent variables with reduced dimensional dynamics. SIMs utilize state space models as a compact representation of multivariate time series data (Akaike, 1975). Canonical variate analysis (CVA) (Larimore, 1990) and subsequent methods such as N4SID extended the work of Akaike to include exogenous variables (Van Overschee and De Moor, 1994). Russell, Chiang, and Braatz (2000) further utilized the canonical variates for process monitoring and fault detection.

To extract predictable DLVs, dynamic inner PCA (DiPCA) algorithm (Dong and Qin, 2018) was introduced to maximize the covariance between the DLVs and their predictions. Later, a dynamic inner canonical correlation analysis (DiCCA) algorithm (Dong et al., 2018) that maximizes the canonical correlations of the DLVs and their predictions is proposed. However, these methods build univariate AR models that extract self-predicting DLVs without interactions among the DLVs. In other words, the latent models are restrictive when interactions exist among the DLVs. Therefore, a recent work is proposed to extract the interacting DLVs through a vector AR model with a CCA objective (LaVAR-CCA) (Qin, 2022). Nevertheless, the latent dynamics are modeled via higher-order AR, which requires many parameters.

While subspace identification methods can be interpreted as latent variable methods for the case of first order dynamics with the number of state variables less than the measurement variables, there is little effort in the literature that focuses on reduced dimensional DLVs with high order dynamics for the DLVs. In this paper, we develop a new algorithm to estimate the latent dynamics with parsimonious latent state space (LaSS) models with general noise dynamics. Dimension reduction and fully interactive DLVs are modeled simultaneously. The LaSS model is estimated via an iterative optimization procedure between the estimation of latent dynamics and the projection for dimension reduction. The latent state dynamics are estimated via a subspace identification method, which is more general than the autoregressive models.

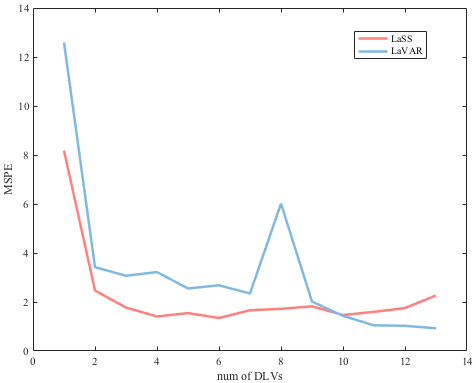
The proposed LaSS algorithm is tested on a chemical process under real operation and compared with the LaVAR algorithm in terms of model accuracy and number of model parameters. The mean squared prediction error (MSPE) of both methods on the test dataset are plotted in the attached figure. LaSS generally outperforms LaVAR with fewer DLVs, which makes the model more concise and efficient in capturing latent dynamics for high dimensional data in chemical processes.

References

Epstein, I. R., & Pojman, J. A. (1998). An introduction to nonlinear chemical dynamics: oscillations, waves, patterns, and chaos. Oxford university press.

Qin, S. J., Dong, Y., Zhu, Q., Wang, J., & Liu, Q. (2020). Bridging systems theory and data science: A unifying review of dynamic latent variable analytics and process monitoring. Annual Reviews in Control, 50, 29-48.

Jolliffe, I. T., & Cadima, J. (2016). Principal component analysis: a review and recent developments. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 374(2065), 20150202.

Krämer, N., & Sugiyama, M. (2011). The degrees of freedom of partial least squares regression. Journal of the American Statistical Association, 106(494), 697-705.

Negiz, A., & Çlinar, A. (1997). Statistical monitoring of multivariable dynamic processes with state‐space models. AIChE Journal, 43(8), 2002-2020.

Box, G. E., & Tiao, G. C. (1977). A canonical analysis of multiple time series. Biometrika, 64(2), 355-365.

Lam, C., & Yao, Q. (2012). Factor modeling for high-dimensional time series: inference for the number of factors. The Annals of Statistics, 694-726.

Peña, D., Smucler, E., & Yohai, V. J. (2019). Forecasting multiple time series with one-sided dynamic principal components. Journal of the American Statistical Association.

Akaike, H. (1975). Markovian representation of stochastic processes by canonical variables. SIAM journal on control, 13(1), 162-173.

Larimore, W. E. (1990). Canonical variate analysis in identification, filtering, and adaptive control. In 29th IEEE Conference on Decision and control (pp. 596-604). IEEE.

Van Overschee, P., & De Moor, B. (1994). N4SID: Subspace algorithms for the identification of combined deterministic-stochastic systems. Automatica, 30(1), 75-93.

Evan L. Russell, Leo H. Chiang, Richard D. Braatz (2000), Fault detection in industrial processes using canonical variate analysis and dynamic principal component analysis,

Chemometrics and Intelligent Laboratory Systems, 51(1), 81-93.

Dong, Y., & Qin, S. J. (2018). Dynamic latent variable analytics for process operations and control. Computers & Chemical Engineering, 114, 69-80.

Dong, Y., Qin, S. J., & Boyd, S. P. (2021). Extracting a low-dimensional predictable time series. Optimization and Engineering, 1-26.

Qin, S. J. Latent Vector Autoregressive Modeling and Feature Analysis of High Dimensional and Noisy Data from Dynamic Systems. AIChE Journal, e17703.