(687c) Hybrid Optimisation of Flow Reactor Performance: A Combined Mechanistic and Data-Driven Approach Using Model-Based Design of Experiments and Gaussian Processes

Kinetic modelling has become an indispensable tool in the industry for a quantitative understanding of reaction systems. A reliable kinetic model can potentially be used to predict the behaviour of the system outside of the experimental conditions used in the model validation and then be used for design, optimization and control in systems engineering applications [1]. However, the kinetic model that describes the physical system may suffer from both parametric and structural uncertainty. Such issues are well known to be present when kinetic models are used in the scale-up of chemical processes when models developed at the lab-scale are used at the pilot or plant scale. The conditions in the lab-scale environments are usually very well controlled and often cannot be guaranteed in the scaled-up process. Furthermore, phenomena such as catalyst deactivation, measurement/control system malfunctions and mass transfer limitations may lead to inaccurate predictions, even though the chemical kinetics and mechanisms have been correctly identified. As a result, the nominal model may lead to a substantial miscalculation of optimal design solutions [2]. To address this issue black-box optimization techniques have been proposed to address the plant-model mismatch [3], where efficient sampling is employed (via the optimization of an acquisition function). However, in many cases, both large design spaces and high sampling variability necessitate a large number of experiments. Hence, the critical challenge is to reduce both the number and the duration of the experiments required. Model-based design of experiments (MBDoE) has been widely used to improve parameter precision and model discrimination in highly nonlinear dynamic systems [4] minimizing the number of experiments needed for kinetic model validation. Nevertheless, even after the MBDoE procedure, the nominal model may not be adequate to represent the actual system. Various solutions have been proposed to tackle the optimal experimental design problem in the presence of parametric uncertainty, including the use of unscented transformations [5] and polynomial chaos expansions [6] for efficient uncertainty propagation. However, so far only a few contributions have been proposed tackling the problem of optimal experimental design under structural model uncertainty [7].

In this work, a novel hybrid two-step optimization technique is proposed, which accounts for structural model uncertainty, especially for the cases that the kinetic model is utilized in the scaled-up process. We propose to first perform an MBDoE technique to reduce the parametric uncertainty of the kinetic model as much as possible. The proposed MBDoE is potentially performed in a lab scale where the conditions are well controlled. Following that, the nominal model is used in the uncertain process as the prior mean function of the Gaussian process, and this hybrid model can account now effectively for the plant-model mismatch. We propose the use of Gaussian processes to capture the plant-model mismatch and propagate the uncertainty to the next time instances. The Gaussian process can precisely approximate the probability density function of an underlying system and propagate the uncertainties effectively as well as estimate the variance of the noise and model. Hence, the prior acquired knowledge can effectively be used for the optimization of the scaled-up process.

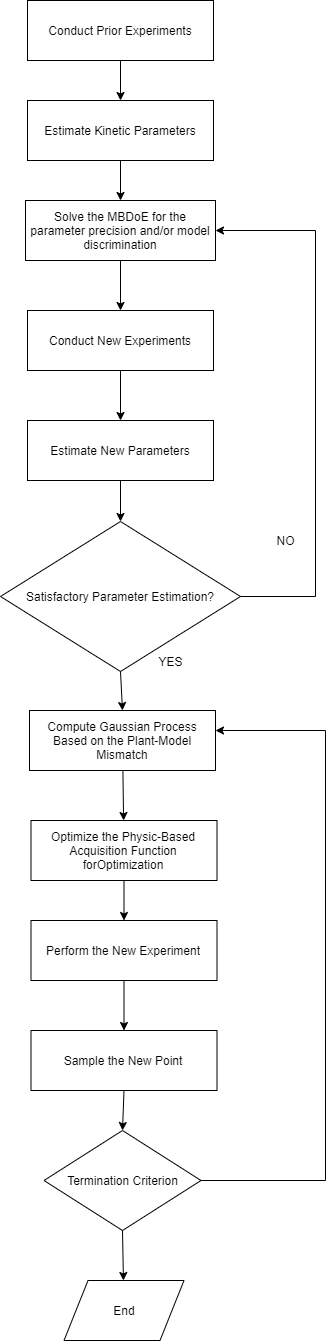
Nevertheless, the hybrid model results in a non-Gaussian distribution that needs to be approximated. Analytical expressions for the covariance of the iterated predictions for multi-step predictions are utilized, allowing the integration of the techniques in an efficient framework. A physics-informed acquisition function is proposed given the hybrid model that takes into account the mechanistic knowledge that is available. Therefore, in an iterative approach, the model parameters are updated, requiring the training of the Gaussian process to capture the new mismatch. The algorithm mentioned above is depicted in Figure 1. The proposed methodology has been applied to the optimization of the online (re)-design of flow reactor to demonstrate the effectiveness of this new algorithm. A nucleophilic aromatic substitution (SNAr) of 2, 4- difluoronitrobenzene with pyrrolidine in ethanol (EtOH) give a mixture of the desired product ortho-substituted, para-substituted and bis-adduct as side products. This case study has been adopted from [8]. The underlying algorithms are implemented in python and CasADi, a dedicated framework for efficient algorithmic differentiation and numerical optimization [9], enabling the fast computations of the proposed optimizations.

[1] Marin G B, Yablonsky G S, Constales D, Kinetics of Chemical Reactions: Decoding Complexity, Second completely revised and enlarged Edition, 2019, Wiley

[2] Petsagkourakis P, Sandoval I O, Bradford E, Zhang D, del Rio-Chanona E A, Reinforcement learning for batch bioprocess optimization, Comput. Chem. Eng., 133 (2020)

[3] Jones D R, Schonlau M, Welch W J, Efficient Global Optimization of Expensive Black-Box Functions, 1998, Journal of Global Optimization, 13, 455–492

[4] Franceschini G, Macchietto S, Model-based design of experiments for parameter precision: State of the art. Chem Eng Sci. 2008, 63(19), 4846 -72.

[5] Telen D, Vercammen, Logist F, Van Impe J, Robustifying optimal experiment design for nonlinear, dynamic (bio)chemical systems, Comput Chem Eng, 2014, 415–25.

[6] Streif S, Petzke F, Mesbah A, R. Findeisen, R.D. Braatz. Optimal Experimental Design for Probabilistic Model Discrimination Using Polynomial Chaos, IFAC Proceedings Volumes (IFAC-PapersOnline), 2017, 19

[7] Petsagkourakis P, Galvanin F, Backoff-Based Model-Based Design of Experiments Under Model Mismatch, Computer Aided Chemical Engineering, 2020

[8] Hone C A, Holmes N, Akien G R, Bourne R A, Muller F L, 2017. Rapid multistep kinetic model generation from transient flow data, Reaction Chemistry and Engineering, 2, 103–108.

[9] Andersson J, Åkesson J, Diehl M, {CasADI}: A Symbolic Package for Automatic Differentiation and Optimal Control. In: Forth S, Hovland P, Phipps E, Utke J, Walther A, editors. Recent Advances in Algorithmic Differentiation. Berlin: Springer; 2012. p. 297–307