(674e) A Hybrid Simulation-Based and Mathematical Optimization Framework: Demonstration on a Carbon Capture System Optimization

This work presents an automated framework for optimization which integrates a modified trust region approach, generation of surrogate models, and a direct link with commercial simulators and algebraic modeling systems. The effectiveness of the proposed approach is demonstrated with two case studies. First, a simple flash model case study is proposed. Secondly, an MEA-based carbon capture system [1] where the reboiler duty was minimized while achieving a 90% capture rate. A comparison with available derivative free optimization methods shows improved solutions in both time and accuracy.

Two main approaches for optimization have been used in carbon capture: 1) pure mathematical optimization and 2) simulation-based optimization. Pure mathematical optimization directly leverages the equations describing the physical system to be optimized. This approach encounters challenges, however, where large sets of PDE’s and highly complex, nonlinear representations are required to sufficiently characterize the process of interest. Simulation-based optimization, on the other hand, considers the system model to be a black box and is based on a heuristic algorithm that uses the results from process simulations to obtain the relationship between the relevant system input and output variables. Although this approach can be used to obtain satisfactory results for large scale, complex systems, it can often be computationally expensive [2]. Hybrid approaches have been proposed in literature [3]; however, their general implementation often requires a very large effort. Considering the advantages and disadvantages of these approaches, a streamlined hybrid framework is introduced to perform efficient optimization of process systems, in terms of solution accuracy, and time.

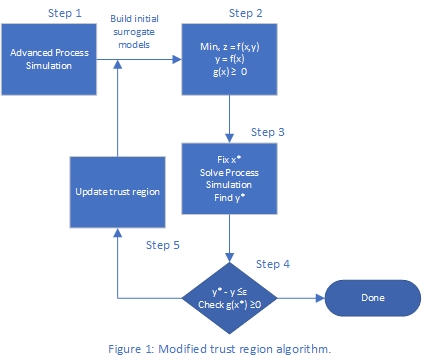
This work is based on a surrogate model (SM)-based optimization algorithm that involves generating a simplified approximation of the rigorous process model (i.e. built using advanced commercial simulators like ASPEN, gPROMs, Python, etc.) that is more amenable to gradient-based optimization methods [4] and nonlinear programming (NLP) solvers. The approach can overcome the difficulties associated with complex process models (for example black box models or rigorous first principle models), without significantly compromising solution quality and speed, provided that the surrogate modeling method is accurate. The proposed work consists of a modified trust region method, which generates complex surrogate models in order to obtain the optimal solution [5]. The proposed framework has been implemented as a capability within NETL’s Framework for the Optimization and Quantification of Uncertainty and Surrogates tool (FOQUS) [6]. The algorithm for the SM-based optimization is highlighted in Figure 1. The algorithm is described in five steps.

Step 1: The algorithm begins with the user providing a process simulation, input and output variables, an initial data set, upper and lower bounds for the optimization variables, and termination conditions. Then, an initial algebraic surrogate model is developed for each output variable for the full space problem (initial data set, set of candidate basis functions, and type of surrogate modeler are selected by the user).

Step 2: Using the initial set of surrogate models and user input (bounds, objective function, ad hoc constraints, etc.), the software builds and solves the mathematical optimization model. The first optimization problem consists of the full-scale problem (original upper and lower bounds of decision variables). Using a multi-start approach, it proceeds to solve multiple problems at different initial conditions, reporting the optimal solution x* and y.

Step 3: The original simulator model is solved at the optimal solution (x*) obtained by the optimization problem. This solution is input into the black box model to determine y* which corresponds to the solution obtained from the advanced process simulator model.

Step 4: This is followed by a set of termination conditions to check whether the optimal solution of the surrogate model is in good agreement with the simulator model (y*). If this condition is satisfied, and the constraints are satisfied, the algorithm is terminated. However, if the termination conditions are not satisfied, the trust region is updated.

Step 5: The trust region is updated by reducing the upper and lower bounds on the decision variables, generating a new data set using Latin Hypercube sampling method, re-running the advanced process simulation for the new data set, and generating a new set of surrogate models.

The algorithm will repeat steps 2 to 5 until convergence. A summary of each algorithm iteration and the final optimal solution are provided, along with a file containing the surrogate models built at each iteration, and a python file containing the parity plots for surrogate model validation.

The algorithm performance is compared against the derivative free optimizers available within FOQUS using two case studies. The first case study entails optimizing a simple flash model simulated in Aspen Plus [7]. The process model includes 59 variables and equations that get solved for simulation in Aspen Plus. Here, the revenue ($/hr) from selling two products is maximized, subject to a CO₂ purity constraint on the vapor stream. In this example, the DFO (based on NLOpt) and SM algorithms find the same optimal solution, though the SM-algorithm converges far more quickly (128 vs. 358 CPU-seconds).

The second case study entails optimizing an MEA carbon capture system model simulated in Aspen Plus. The process model includes 46071 variables and equations that get solved for simulation in Aspen Plus. In the second case study, an MEA carbon capture simulation is solved to optimality more quickly using the SM-algorithm compared with DFO solver (48 vs. 65 CPU-minutes). Additionally, the SM-algorithm finds a better optimal solution, which would translate in large savings during a year of operation.

Compared with DFO’s, the algorithm presented is expected to show better performance (time and solution accuracy) when larger problems are studied. Finally, the proposed approach presents a generic framework for rigorous optimization of large-scale nonlinear systems.

References

[1] Morgan, J.C., Soares, C.A., Omell, B., Bhattacharyya, D., Tong, C., Miller, D.C. (2018). Development of a rigorous modeling framework for solvent-based CO2 capture. Part 2: Steady-state validation and uncertainty quantification with pilot plant data. Industrial & Engineering Chemistry Research 57: 10464-10481.

[2] Larson, J., Menickelly, M., Wild S. M. Derivative-Free Optimization Methods. Optimization Online. http://www.optimization-online.org/DB_FILE/2019/04/7153.pdf

[3] Lee, U., Burre, J., Caspari, A., Kleinekorte, J., Schweidtmann, A.M., Mitsos, A. (2016) Techno-economic Optimization of a Green Field Post-Combustion CO2 Capture Process Using Superstructure and Rate-Based Models. Industrial & Engineering Chemistry Research. 12014-12026.

[4] Cozad, A., Sahinidis, N., Miller, D.C. (2014). Learning Surrogate Models for Simulation-Based Optimization. AIChE Journal 60(6): 2211-2227.

[5] Eason, J. P., Biegler L. T. (2016). A Trust Region Filter Method for Glass Box/Black Box Optimization. AIChE Journal. 3124-3136.

[6] Miller, D. C., Agarwal D. A., Bhattacharyya D., Boverhof J., Cheah Y-W., Chen Y., et al. (2016). Innovative computational tools and models for the design, optimization and control of carbon capture processes. 26th European Symposium on Computer Aided Process Engineering – ESCAPE 26. 2391-2396

[7] Aspen Plus V8.0 – Optimization Tutorial, Merten Morales, Swiss Federal Institute of Technology Zurich (Aug 2013)