(578h) On the Acceleration of quadratic Semidefinite Outer-Approximation Using Combinations of Cutting Plane Approximations and Data Analytics

Misener and co-workers have pioneered effective outer-approximations for quadratic semidefinite relaxations where they retain most of the relaxation tightness in the form of sparse (low-dimensional) linear cuts well-suited for Branch and Cut algorithms. They subsequently formulate low-dimensional semidefinite decompositions for outer-approximation via matrix completion and optimality based cutting planes. Lugojan, Misener et al. (2018)[1] proposed the novel approach to solve quadratic optimization problems using an online selection of low-dimensional linear cuts from Semidefinite Programming (SDP) relaxations. Starting from an N-D space, the central idea involves a preliminary stage to sparsify the problem and to subsequently develop cutting planes that would consider smaller n-D sub-sets as sub-problems. The combinations of subsets are expected to explode with large and jumbo instances (80<N<125) or low dimensionality cuts( 3<n<5). Then, a selection of the sub-sets is necessary to generate hyperplanes. That was achieved using an off-line trained NN that produced populations of hyperplane candidates that should be evaluated and subsequently incorporated in the primal problem. Cutting planes previously used in linear outer-approximations have been of high [2] and medium dimensions [3]. In the state-of-the-art algorithm[1] the selection of subs-sets included options for feasibility (through eigenvalues: f1) and optimality (projected improvement of the objective function, f2). While performance criteria are applied on each individual candidate in the population, relationships between candidate sets and their complementarity in covering the solution space have never been addressed.
The aim of the study has been to accelerate the performance of the approach against the state-of-the-art by addressing completeness in the selection of cutting planes, subsequently exploring online improvements in the Separation Problem. To that extent, the paper illustrates significant improvements against the state of the art for a wide range of problems that vary in size (70-125 dimensions) and sparsity (25-75% density). Given the populations (P) and the subsets generated by the sparsification stages, an approach is proposed to commit cut selection to data analytics thus connecting the method with emerging technologies in data models and machine learning.
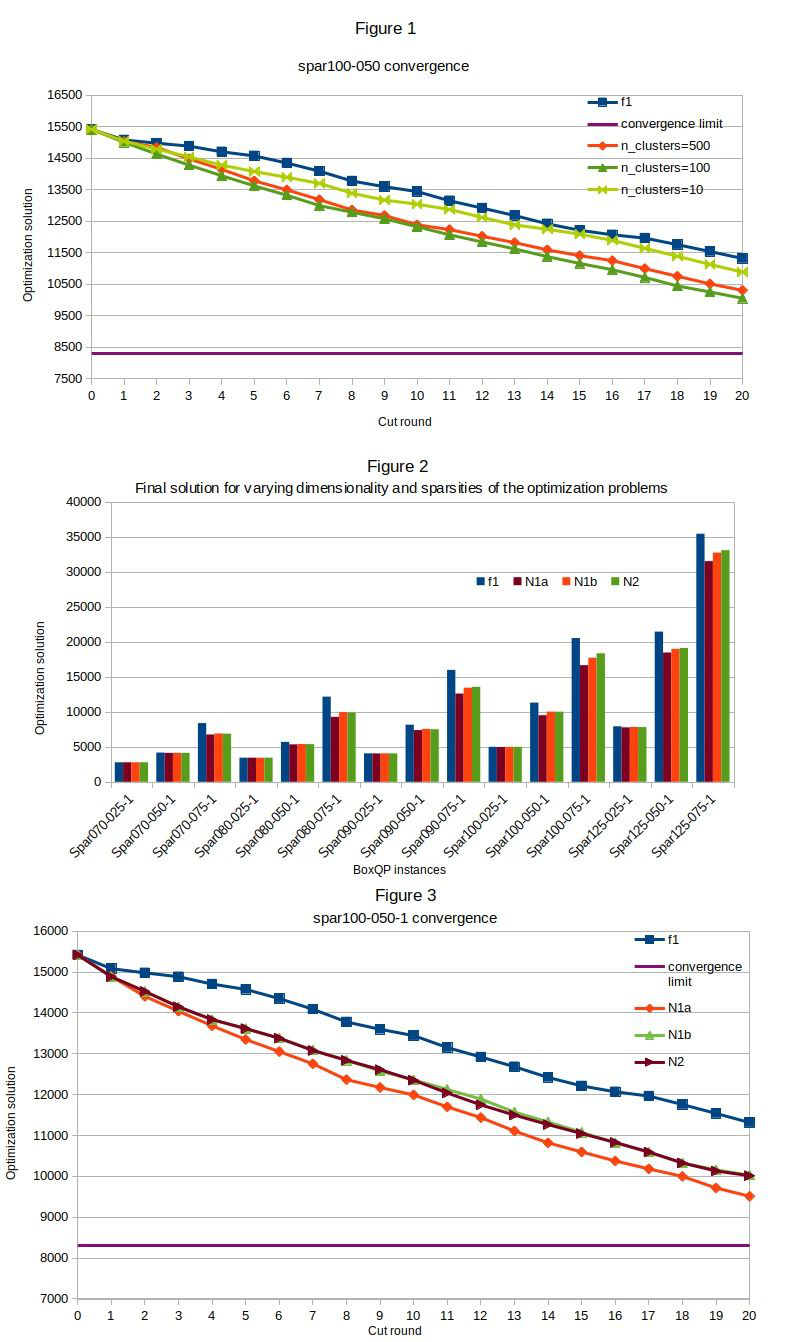
The approach used the same number of cutting planes with the state-of-the-art. The reference population (P) contains 3D projections on which cutting planes are produced. Consistent with conventions in the original paper [1], the ‘convergence limit’ corresponds to solutions using: f1, 40 cut rounds and 5% selection sizes from available cutting planes. The approach addressed the problem in two separate stages. The first stage considered over-the-self clustering technology using several variants and the Euclidean norm. The approach was tested with fixed and variable-size clusters (10-500); various criteria in selecting populations for different clusters (1-10 cuts/cluster). Besides general improvements over the state-of-the-art, performance gains have been marginal and erratic. Figure 1 illustrates results using clusters of fixed sizes. Better results have been produced with cluster populations close to the size of the sub-sets (e.g. 100); smaller and larger cluster sizes produced worse results.
The second stage replaced the Euclidean norm and used a weighted norm that compounds differences in the type of variables involved at each sub-set (discrete, N1) and their projected states (continuous, N2). The rationale in the alternative norm has been to assist in spreading out the sub-sets over the full space rather than stow and congest candidates in adjacent locations. Results are summarized in Figure 2 and illustrate, with a single exception at low density instances, consistent and significant improvements in all problems examined problems. The comparison addressed the final solution obtained over the same number of cut rounds. The norms have been applied separately or in compounded form. N1 has been applied in two variants; they both yield similar improvements. Although consistently inferior, N2 is still always better than the state-of-the-art. Figure 3 focuses on a jumbo and medium density instance suggesting that the proposed norms have a faster convergence than f1 and overall converge in a lower bound than f1.
Work in progress addresses means to discover similarity patterns across iterations, the development of memory trails and means to accelerate the algorithms in terms of convergence at execution time. Keeping memory of the iterations and projecting data from each round in the same space could be achieved using a space reduction model such as a learning manifold or even unsupervised clustering.
Bibliography
[1] Radu Baltean-Lugojan, Ruth Misener, Pierre Bonami and Andrea Tramontani. Selecting cutting planes for quadratic semidefinite outer-approximation via trained neural networks. 2018. https://github.com/rb2309/SDPCutSel-via-NN
[2] A. Qualizza, P. Belotti, and F. Margot. Linear programming relaxations of quadratically constrained quadratic programs. In J. Lee and S. Leyffer, editors, Mixed Integer Nonlinear Programming, volume 154 of The IMA Volumes in Mathematics and its Applications, pages 407–426. Springer New York, 2012.
[3] H. D. Sherali and B. M. P. Fraticelli. Enhancing RLT relaxations via a new class of semidefinite cuts. Journal of Global Optimization, 22(1-4):233–261, 2002.