(541d) Handling a Class of Non-Convexities in MINLP for Utility Optimization

Extended Abstract

Utility optimization is an important operational step in chemical process industry where multiple sources can supply energy to meet process operational requirements. Units such as turbines, boilers, chiller plants, brine plants, hot oil generators should run continuously to meet process demand. Continuous production requirements with multiple energy sources that are either endemic or external to the process poses the optimization problem of selecting economical sources while meeting process constraints.

Conventionally, the energy optimization problem is represented by a system of nonlinear equations that represent the plant and is solved as a continuous nonlinear programming (NLP) problem. Most NLP algorithms work best in the neighborhood of an operating point and will not explore solutions that requires distant excursions from the current equilibrium. If a source that is endemic to the process is loaded because of economics, the process equilibrium can change, further complicating the solution with NLP due to changed scaling of the problem space. For successful operation, NLP solvers require initialization with suitable scaling in a small, continuous, locally convex neighborhood of the solution. Utility optimization cannot always guarantee such conditions, thereby posing a challenge for NLP.

Mixed-integer nonlinear programming (MINLP) optimization has the capability to switch in and out energy-supplying units, depending on the economics, energy and material balance, and underlying nonlinear-process optimality. Typical MINLP algorithms harness an NLP solver to find the local optimum at each node in the exploratory path of a branch and bound method [1].

A solution to the MINLP utility optimization problem involves the selection of the most economical energy sources, switching off unproductive work streams, and turning on productive work streams, and turning off expensive energy sources. The process of switching sections of the flow-sheet is done using binary switches that function to turn on or off entire process units. These binary variables – termed MINLP switches - are determined by the MINLP algorithm.

Process flow-sheets typically incorporate operating specifications and variable bounds, to represent plant operating conditions and constraints. Specifications are fixed independent variables that process models must support while operational. Specifications and variables with restrictive non-zero lower bounds prevent the process models from turning off in MINLP, in order to obey those constraints. These form non-convex barriers to the operation of the NLP when directed to solve such process units down to zero-state. Such non-convexities lead to convergence-failures of the underlying NLP, resulting in incorrect branch-and-bound pruning of the nodes under this failing node, thereby converging to sub-optimal MINLP solutions. Our goal is to expand the region of convergence of the underlying NLP algorithm by appropriate modification of these non-convexities.

In this paper, we report results with a reduced-gradient, infeasible-path, active-set, sequential quadratic programming nonlinear solver [2] in conjunction with the MINLP branch-and-bound solver framework [1].

We discuss methods to overcome convergence difficulties arising from the non-convexities of restrictive specifications and non-zero lower bounds and obtain better solutions for structural and parameter optimization of utility plants that satisfy given electrical, mechanical and heating demands of industrial processes. The key methods proposed are local convexification by the modification of relevant process model equations, to discount the impact of a restrictive fixed specification or a non-zero lower bound. Such equation-based local convexification is well known in academia, see for example, [3]. Our contribution is in the identification of non-convexities in the utility optimization equations of various process units, and the development of appropriate local convexification schemes.

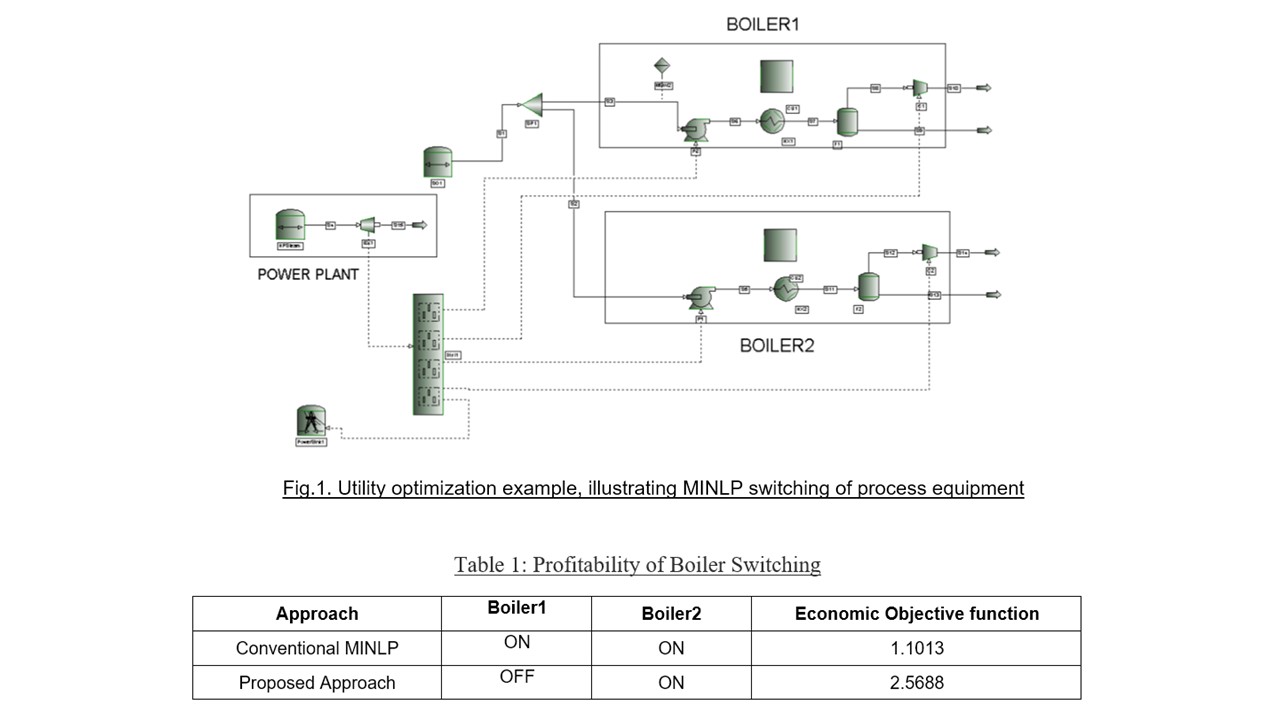
Fig.1 shows a switchable utility optimization case study used to demonstrate the proposed methods.

In the flow-sheet shown in Fig.1, fresh water is taken in the source unit. A splitter is used to feed water evenly in both boiler systems. A boiler is constructed with a heat exchanger followed by a flash and compressor. The flash unit ensures vapor feed to compressor and takes out the liquid. The compressor in Boiler1 has lower efficiency than the one in Boiler2. Attaching an MINLP switch to the Boiler1 feed pump enables the algorithm to consider the attached variable as a switchable. This switch is associated with the molar flow of that stream. The units in the boiler system that require power are connected to a distributor. The power plant supplies electric power to the distributor and a power sink sells the power to the grid. The objective of MINLP is to maximize the sink power which will maximize profit, while maintaining process operational constraints.

The test setup considers different specifications on the compressors such as outlet-pressure, head, pressure-rise, pressure-ratio and work, representing different duty-cycles. The economics is set conservatively so that Boiler1 should turn off while Boiler2 should pick up the workload at an optimal solution.

The flow-sheet described above experiences convergence difficulties in turning off the inefficient boiler, due to restrictive local non-convexities encountered at the zero-state of the process units of Boiler1.

A sample result is shown in Table 1.

Table 1 shows that a conventional MINLP application that has not done local convexification would not be able to turn off Boiler1 due to its operational constraints. With the proposed local-convexification modifications, Boiler1 can be turned off, attaining the optimal solution.

Boiler1 incurs higher operating cost and reduced profit due to its lower efficiency. The restrictive lower bound on the specification of compressor-work did not allow the conventional MINLP algorithm to take power input to Boiler1’s compressor to zero due to failure of the underlying NLP, and it remains turned on. With the proposed approach we overcome the restriction to turn off Boiler1 and the total flow is diverted to Boiler2. The impact is clearly observed in economic objective function in Table 1.

Conclusion

This paper addresses utility optimization of processes with local non-convexities arising from operational constraints. We address two common operating constraints - fixed independent specifications and restrictive lower bounds on variables, both of which cause NLP algorithm failures especially when the MINLP node directs those process units to be turned off. Such false failures of the NLP cause incorrect pruning of the branch-and-bound tree, preventing the MINLP algorithm from finding optimal solutions. Through local convexification of the relevant process model equations, we demonstrate successful operation of the underlying NLP algorithms when directed to solve to zero-state, even in the presence of restrictive real-world operational requirements. This allows a greater successful exploration of the solution space by MINLP algorithms, leading to higher-quality solutions with better profitability, than without such modifications.

References

[1] An algorithmic framework for convex mixed integer nonlinear programs, P Bonami, LT Biegler, AR Conn, G Cornuéjols, IE Grossmann, CD Laird, J Lee, A Lodi, F Margot, N Sawaya, A Wachter, Discrete Optimization, Vol 5, Issue 2, 2008, pp. 186-204.

[2] SimSci ROMeo Process Optimization, Retrieved from https://sw.aveva.com/operate-and-optimise/optimise-operations/romeo-proc..., April 2020.

[3] R. Porn, I. Harjunkoski, T. Westerlund, “Convexification of different classes of nonconvex problems”, Computers & Chemical Engineering, Vol 23, Issue 3, Feb 1999, Pp. 439-448