(431a) Spherical Agglomeration: Process Modelling and Validation for Kinetic Estimation

Background

Manufacturing particulate products with optimal performance requires tightly controlled processes across several industries such as pharmaceuticals. A key unit operation at the drug substance to drug product interface is crystallisation which is a critical separation and purification technique for the recovery of active pharmaceutical ingredients. It is therefore essential to understand and control crystal properties as they have shown to strongly impact downstream processes and the manufacture of pharmaceutical tablets [1].

Spherical agglomeration (post-crystallisation) is an emerging particle formation method which has the capability to improve problematic particle shapes (needles, rods, flakes) and increase particle size [2]. This involves the controlled addition of a partially-miscible solvent termed the bridging liquid to pre-suspended crystals through a single intensified unit operation. The bridging liquid should have a high affinity with the drug to agglomerate the crystals and under optimised conditions, compact and dense spherical agglomerates are produced. As a result, the produced agglomerates display high bulk densities, better flow properties, easier filtration and downstream processing in addition to suitability for direct compression of active pharmaceutical ingredients [3].

Process Modelling

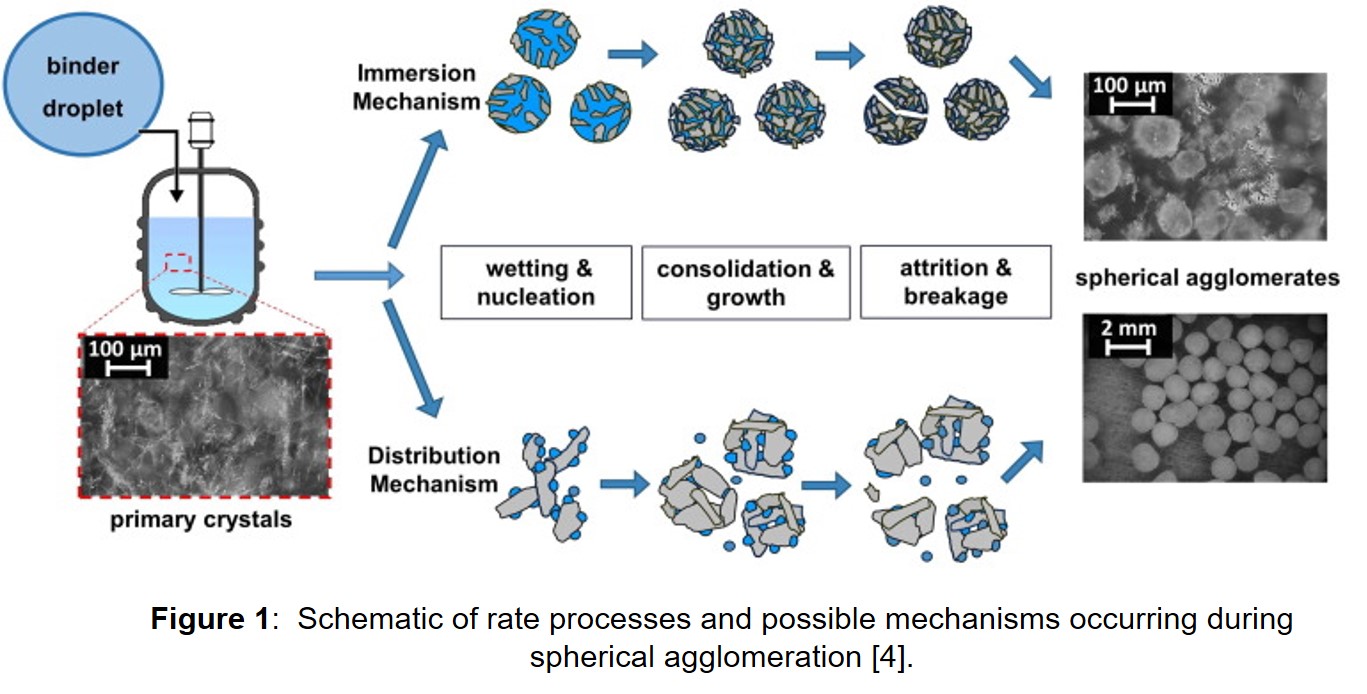
Analogous to wet granulation mechanisms, spherical agglomeration exhibits different rate processes: wetting/nucleation of primary crystals by the bridging liquid, consolidation/growth of agglomerate nuclei, and attrition/breakage of the agglomerates through an immersion and distribution mechanism (Figure 1). A recent novel mathematical model was developed to predict kinetics and formation of agglomerate nuclei occurring in an immersion spherical agglomeration process [4]. Importantly, three different regimes for agglomeration nucleation were found; immersion rate limited regime, collision rate limited regime and intermediate regime. The mechanistic model was then successfully integrated along with key material properties and process parameters into a gPROMS FormulatedProducts® (PSE) flowsheet to develop a population balance model framework.

The aim of this work is to identify and assess the impact of material attributes, equipment and process parameters on product attributes through population balance modelling. The influence of key input model parameters such as the bridging liquid mean particle, liquid flow rate and addition time on the particle size, size distribution and porosity is investigated. Furthermore, characteristic process trends such as initiation and duration of nucleation are studied. As such, a comprehensive sensitivity analysis will be evaluated for risk mitigation approaches and greater process understanding of the predictive model. For kinetic estimation and model validation, carefully designed small-scale decoupled experiments will be performed to account for the different rate processes in spherical agglomeration.

References:

1. Variankaval, N., A.S. Cote, and M.F.J.A.J. Doherty, From form to function: Crystallization of active pharmaceutical ingredients. 2008. 54(7): p. 1682-1688.
2. Pitt, K., et al., Particle design via spherical agglomeration: A critical review of controlling parameters, rate processes and modelling. 2018. 326: p. 327-343.
3. Amaro-González, D. and B.J.P.t. Biscans, Spherical agglomeration during crystallization of an active pharmaceutical ingredient. 2002. 128(2-3): p. 188-194.
4. Arjmandi-Tash, O., et al., A new mathematical model for nucleation of spherical agglomerates by the immersion mechanism. 2019. 4: p. 100048.