(411c) A General Framework for Simultaneous Quantification of Parametric and Structural Model Uncertainty

Over the last few years, the process industries have showed growing interest in the use of computational techniques for the optimization of process operations. This trend is confirmed through the industry 4.0 paradigm, which calls for the systematic use of model-based monitoring, control and optimization for improving product quality [1] as well as process economics [2], reliability and safety [3]. It is important to note that this new reliance on computational tools to optimize industrial operations is not limited to the process industries (it is already affecting other industrial sectors such as pharmaceutical manufacturing and the food industry), thus is expected to continue in the years to come. Therefore, we can envision that model-based monitoring, control and optimization will become the backbone of industry practices in the near future.

A key challenge in the systematic implementation of the industry 4.0 goals is the lack of process models, accurate and reliable enough for purposes of process optimization. In fact, the predictions of every mathematical model are affected by both structural and parametric uncertainty, which must be quantified and explicitly considered in most monitoring, control and optimization applications, in order to fully exploit the benefits offered by these advanced process management strategies. Unfortunately, to this day, there are no general methods for the simultaneous quantification of both structural and parametric model uncertainty, thus this research area still offers significant challenges and opportunities.

In view of these considerations, we propose an innovative framework for the simultaneous quantification of both structural and parametric model uncertainty, applicable to any type of process model (NLS, ODE, DAE, etc.). Given a set of structurally different candidate models (i.e., a superstructure of model components) and process data (i.e., time series of experimental measurements), the proposed framework follows this rationale:

1. First, we utilize appropriate data smoothing techniques to identify temporal trends in the process data.
2. Then, we compute a structural uncertainty index for every candidate model by multi-objective optimization (structural uncertainty is measured as the discrepancy between experimental and model trends).
3. Next, we calculate a parametric uncertainty index for every candidate model through Bayesian inference (this step requires estimation of the probability distribution of the parameters of every model).
4. Finally, we combine the structural and parametric uncertainty indices into an overall uncertainty score, which allows selection of the best model (the latter is the model associated with the smallest overall uncertainty score).

Once the best model has been identified, we can utilize the quantities, computed in steps a-d, to readily estimate any other uncertainty measure (e.g., joint, marginal and conditional probability distributions of the model parameters and states as well as any of their central tendency and dispersion measures), which is more appropriate for the final application of interest (e.g., process design, monitoring, control and optimization under uncertainty).

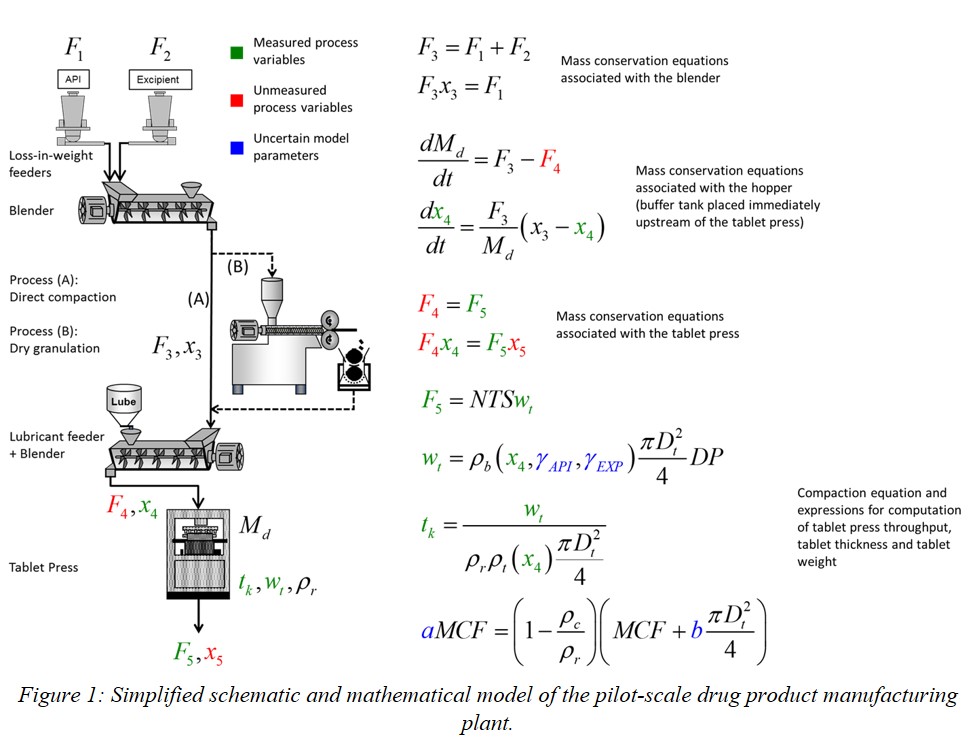
This novel approach to the simultaneous quantification of parametric and structural model uncertainty is demonstrated on two different processes, specifically a continuous stirred tank reactor and a pilot-scale plant for producing oral drug doses (Figure 1). In both case studies, we solve risk-based decision making problems under both structural and parametric model uncertainty, in which the objective is to isolate and reject off-spec products in real time, before they contaminate the on-spec production. The results of these studies confirm that the frequency of false positives (rejection of on-spec product) and false negatives (acceptance of off-spec product) can be reduced by explicitly accounting for the presence of structural uncertainty in the process model, as opposed to the conventional assumption of negligible structural uncertainty.

References:

[1] Mockus, L., Laínez, J. M., Reklaitis, G., & Kirsch, L. (2011). A Bayesian Approach to Pharmaceutical Product Quality Risk Quantification. Informatica, 22(4), 537-558.

[2] Rossi, F., Reklaitis, G., Manenti, F., & Buzzi-Ferraris, G. (2016). Multi-scenario Robust Online Optimization and Control of Fed-batch Systems via Dynamic Model-based Scenario Selection. AIChE Journal, 62(9), 3264-3284.

[3] Rossi, F., Manenti, F., Buzzi-Ferraris, G., & Reklaitis, G. (2017). Combined dynamic optimization, optimal control and online runaway detection & prevention under uncertainty.