(109a) Optimization-Driven Quasi-Deterministic Monte Carlo Sampling for Accurate Uncertainty Quantification: Applications to the Pharmaceutical Industry

Numerical algorithms for estimation of probability distributions are the backbone of advanced process design, monitoring and optimization techniques, e.g. stochastic dynamic optimization (Rossi et al., 2016), robust state estimation (Mondal et al., 2010) and real-time risk-based decision making (Si et al., 2012). The latter have recently attracted the attention of both industry and academia, due to the emergence of the industry 4.0 paradigm and the steady increase in the availability of readily accessible experimental and process data. In view of these considerations, the development of new and more efficient methods for PDF estimation could facilitate the systematic implementation of the industry 4.0 guidelines, thus improving process automation, economics, reliability and safety.

Most of the conventional algorithms for estimation of probability density functions (PDFs), e.g. Metropolis-Hastings, Gibbs sampling and Hamiltonian Monte Carlo (Gamerman and Lopes, 2006), consist of Monte Carlo sampling strategies, which rely on acceptance/rejection criteria to draw samples from the high probability regions of the PDF of interest. These algorithms are well-established, reasonably accurate and generally reliable but suffer from some important drawbacks: (I) poor performance in the presence of high parameter correlation; (II) limited applicability to complex PDF estimation problems (these state-of-the-art algorithms may not properly capture the features of multimodal PDFs, heavily skewed PDFs and/or PDFs with non-convex level sets); (III) considerable (often unaffordable) computational cost; and (IV) poor scalability and limited intrinsic concurrency. Unfortunately, probability distributions with complex shapes and high parameter correlation are very common in engineering applications, thus there is a need for new algorithms for estimation of probability distributions, which can mitigate some of the aforementioned drawbacks.

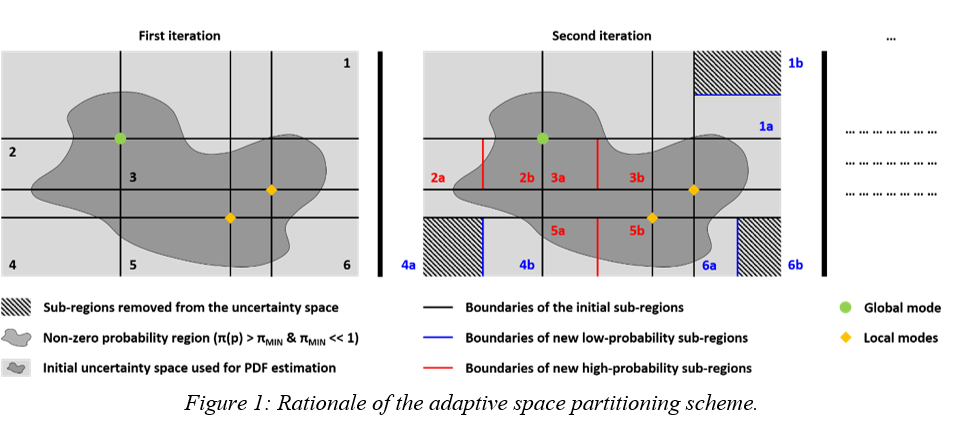
This contribution proposes a new strategy for PDF estimation, which combines an adaptive space partitioning scheme, inspired by multidimensional integration algorithms (Hahn, 2005), with a quasi-deterministic sampling method, based on optimization. Adaptive space partitioning alternates with optimization-driven sampling in an iterative fashion, until appropriate convergence conditions are met, e.g. the sample moments of the probability distribution of interest no longer vary between consecutive iterations. The adaptive cubature step serves three principal purposes (Figure 1): (I) identification of those regions of the uncertainty space (the space spanned by the parameters of the probability distribution of interest), in which the current estimate of the PDF requires further refinement; (II) detection of very low probability density regions, which can be safely ignored; and (III) improvement of the concurrency and overall computational efficiency of the algorithm (sampling can be conducted in parallel within different subregions). The optimization-driven sampling phase complements the former, in that it allows selection of optimal samples, which uniformly span every single subregion of the uncertainty space, without the need for acceptance/rejection schemes, which often accept only a small fraction of all the candidate samples analyzed. As consequence of the combination of adaptive space partitioning and quasi-deterministic, optimization-driven sampling, the proposed PDF estimation method can generate accurate estimates of complex PDFs at reasonable computational cost, is generally insensitive to parameter correlation, and exhibits better scalability features than similar state-of-the-art algorithms.

The new PDF estimation strategy, proposed in this contribution, has been demonstrated on several different case studies, namely, the estimation of several known probability distributions as well as the computation of the PDF of the parameters of the mathematical model of a continuous drug product manufacturing plant (the scale of these PDF estimation problems ranges from 2 to 8 dimensions). As a basis for comparison, all of these applications have also been solved with conventional Monte Carlo methods. These case studies confirm that the new PDF estimation strategy, proposed in this work, is more accurate and robust than state-of-the-art Monte Carlo methods.

References

Gamerman, D., Lopes, H.F. (2006). Markov Chain Monte Carlo - Stochastic simulation for Bayesian inference. Taylor & Francis Group, New York (NY).

Hahn, T. (2005). Cuba – a library for multidimensional numerical integration. Computer Physics Communications, 168, 78-95.

Mondal, S., Chakraborty, G., Bhattacharyy, K. (2010). LMI approach to robust unknown input observer design for continuous systems with noise and uncertainties. International Journal of Control, Automation and Systems, 8, 210-219.

Si, H., Ji, H., Zeng, X. (2012). Quantitative risk assessment model of hazardous chemicals leakage and application. Safety Science, 50, 1452-1461.

Rossi, F., Reklaitis, G., Manenti, F., Buzzi-Ferraris, G. (2016). Multi-scenario robust online optimization and control of fed-batch systems via dynamic model-based scenario selection. AIChE Journal, 62, 3264-3284.