(541e) An Mpcc Approach to Robust Optimal Sizing of Thermal Energy Storage with Bidirectional Flows

There is a very large potential for using surplus heat from industrial processes in district heating networks. However, the availability of surplus heat and the heat demand from the district is often asynchronous in nature. Expensive peak-heating sources like fossil fuels or electricity from the grid are typically used to cover this mismatch. In this context, thermal energy storage (TES) is an appealing technology in district heating networks for facilitating dynamic heat integration between heat supply and demand. A long-term strategy from an energy-efficiency perspective must include adequate consideration for the optimal sizing of the TES unit. The common practice in industry is to employ heuristics-based approaches for finding the capacity of TES units. However, these approaches do not consider the short-term variability in the operation profiles of heat supply and demand, thus leading to suboptimal designs that are not robust against uncertainty. To resolve this, a scenario-based stochastic programming approach, where the operational uncertainty is described in the form of discrete scenarios, can be used to find the best design for the TES system.

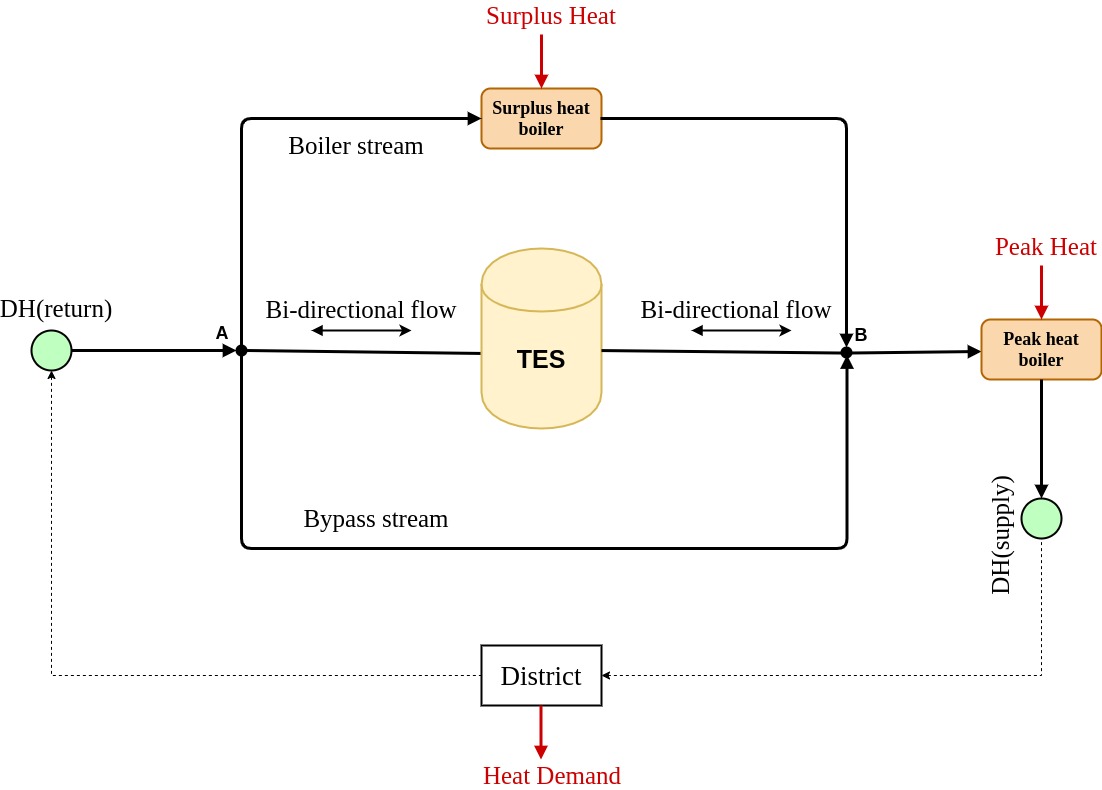
The basic topology of the district heating network, based on a district heating company in northern Norway, is shown in the uploaded figure. The surplus industrial heat is supplied through a surplus heat boiler (SHB). When the available heat is insufficient to satisfy district heating demand, the fossil-based peak heating is supplied through the peak heat boiler (PHB) to heat up the stream to the required temperature. The cold stream returned from the district splits at node A into 3 streams, going to the SHB, the TES, or bypassing directly to the PHB. The flow through the TES is bidirectional, depending on whether the TES is charging or discharging. When the heat supply is greater than the demand, the heat from the outlet of SHB is used to charge the TES (flow from node B to node A). On the other hand, when there is excess demand, the TES discharges the stored heat into the supply stream (flow from node A to node B).

The design objective is to minimize the capital costs associated with the size of the TES unit, and the operation objective is to minimize the use of peak-heating sources. We use a stochastic programming approach where the objective of the optimization problem includes the capital costs and a weighted sum of the operating costs of all scenarios (where each scenario is a combination of a representative heat supply and heat demand profile). The bidirectional flow through the TES is modeled with complementarity constraints, rendering the optimization problem a mathematical program with complementarity constraints (MPCC). The MPCC can be solved by relaxing the complementarity constraints with a square-root approximation parametrized by some ε. The idea is to first solve the problem with a relatively large ε, and to promote convergence by iteratively decrease its value by initializing the solver (Ipopt) with the solution of the previous iteration [1,2]. The process can be sped up by solving the problem for a large ε*, and then taking a parametric NLP-sensitivity step (w.r.t. ε) from ε = ε* to ε = 0 [3]. The solution obtained gives the optimal sizing of the TES unit that is robust against fluctuations in heat supply and demand profiles.

References:

[1] Daniel Ralph & Stephen J. Wright (2004) Some properties of regularization and penalization schemes for MPECs, Optimization Methods and Software, 19:5, 527-556, DOI: 10.1080/10556780410001709439

[2] Leyffer S. (2006) Complementarity constraints as nonlinear equations: Theory and numerical experience. In: Dempe S., Kalashnikov V. (eds) Optimization with Multivalued Mappings. Springer Optimization and Its Applications, vol 2. Springer, Boston, MA

[3] Pirnay, H., López-Negrete, R. & Biegler, L.T. Optimal sensitivity based on IPOPT. Math. Prog. Comp 4, 307–331 (2012). https://doi.org/10.1007/s12532-012-0043-2